Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is $λ$

Video Solution

Text Solution

Verified by Experts

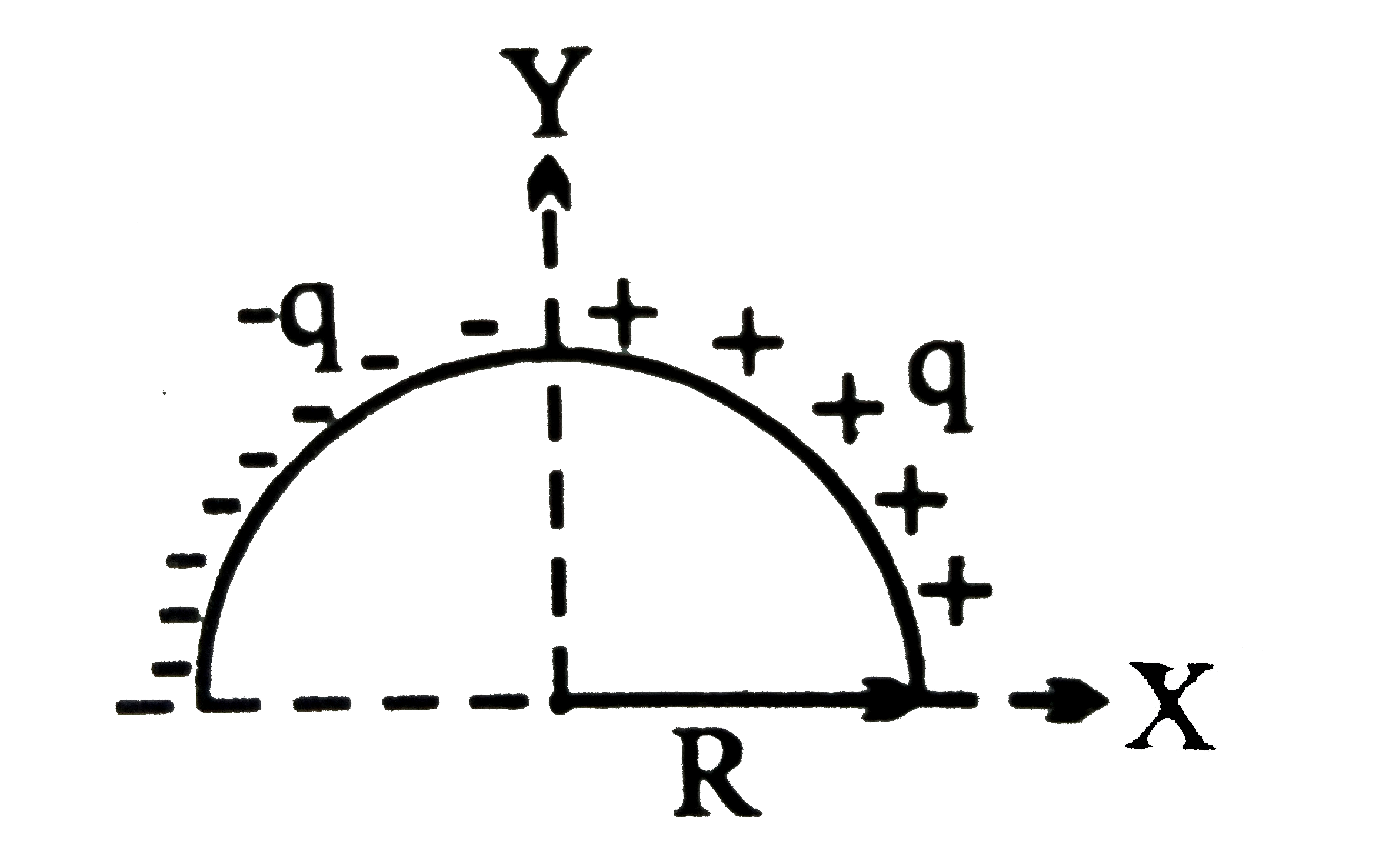
We consider a different elenent dl on the ring that subtends an angle $d θ$ at the center of the ring, i.e. $d l = R d θ$ . So the charge on this element is $d Q = λ R d θ$ . This element creates a field dE, which makes an angle $θ$ at the center as shown in fig.

For each differential element in the upper half of the ring, there corresponds a symmetrically palced charge element in the lower half. the y-components of the field due to these symmetric elements cancle out, and the x-components remain. So we get
$d E_{x} = d E cos θ = \frac{d Q}{4 π ε_{0} r^{2}} cos θ = \frac{λ (R d θ) cos θ}{4 π ε_{0} R^{2}}$
On intergrating the expression for $d E_{x}$ with respect to angle $θ$ in limits $θ = - (π) / 2 \to θ = + π / 2$ we obtain
$E = \int_{- π / 2}^{+ π / 2} \frac{λ R}{4 π ε_{0} R^{2}} cos θ d θ = \frac{λ}{2 π ε_{0} R}$
In terms of the total charge, say Q, on the ring $λ = Q / π R$ and we get $E = Q / 2 π^{2} ε_{0} R^{2}$
If we consider the wire in the form of an are aas shown in fig. the symmetry consideration is not useful in canceling out x- and y- components of the fields , if $θ_{1}$ and $θ_{2}$ are different. We will intergrated $d E_{x}$ as well as $d E_{y}$ in limits $θ = - θ_{1}$ to $θ = - θ_{2}$ .

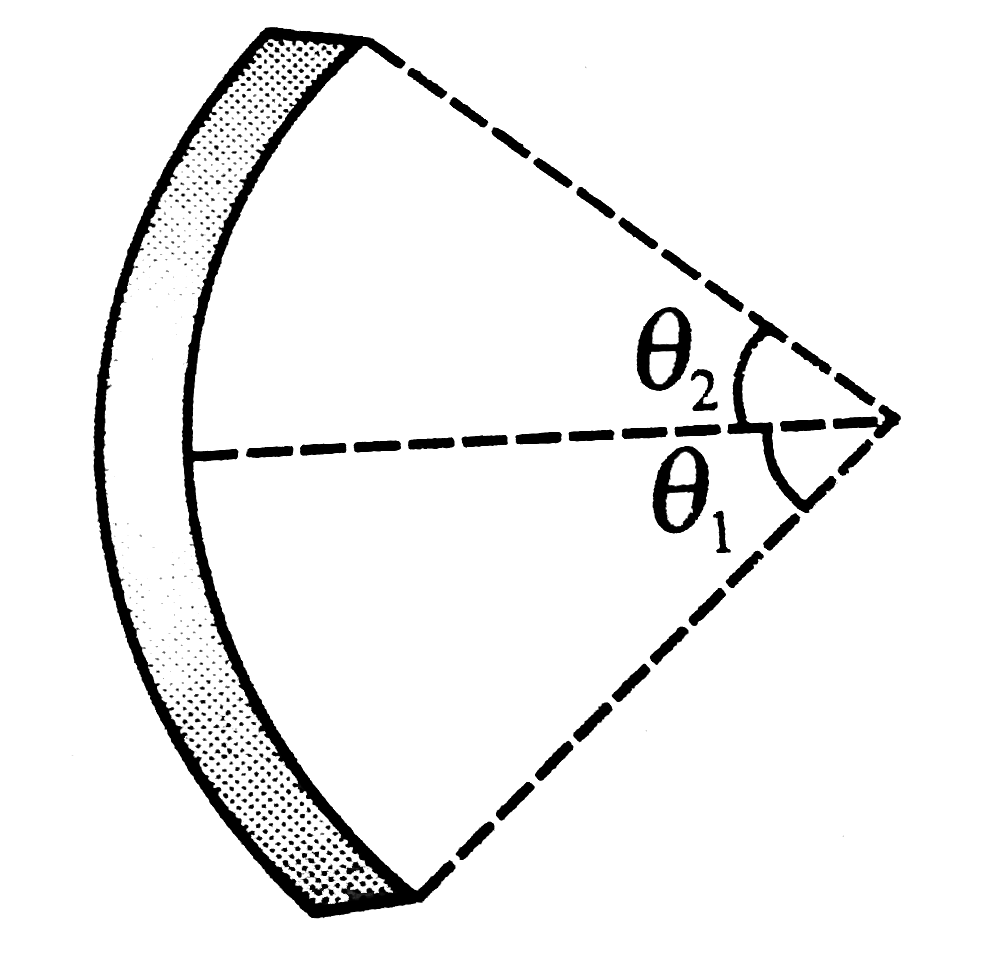
$E_{x} = \int_{- θ_{1}}^{+ θ_{2}} \frac{λ R}{4 π ε_{_} (0) R^{2}} cos θ d θ = \frac{λ}{4 π ε_{0} R^{2}} ({sin θ}_{1} - {sin θ}_{2})$
$E_{y} = \int_{- θ_{1}}^{+ θ_{2}} \frac{λ R}{4 π ε_{0} R^{2}} sin θ d θ = \frac{λ}{4 π ε_{0} R^{2}} ({cos θ}_{2} + {cos θ}_{1})$
For a sysmmetrical are , $θ_{1} = θ_{2}$ . thus $E_{y}$ vanishes and
$E_{x} = \frac{λ sin θ}{2 π ε_{0} R}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-COULOMB LAW AND ELECTRIC FIELD-Single Answer Correct Type

Home
Ask Doubt
Profile