A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
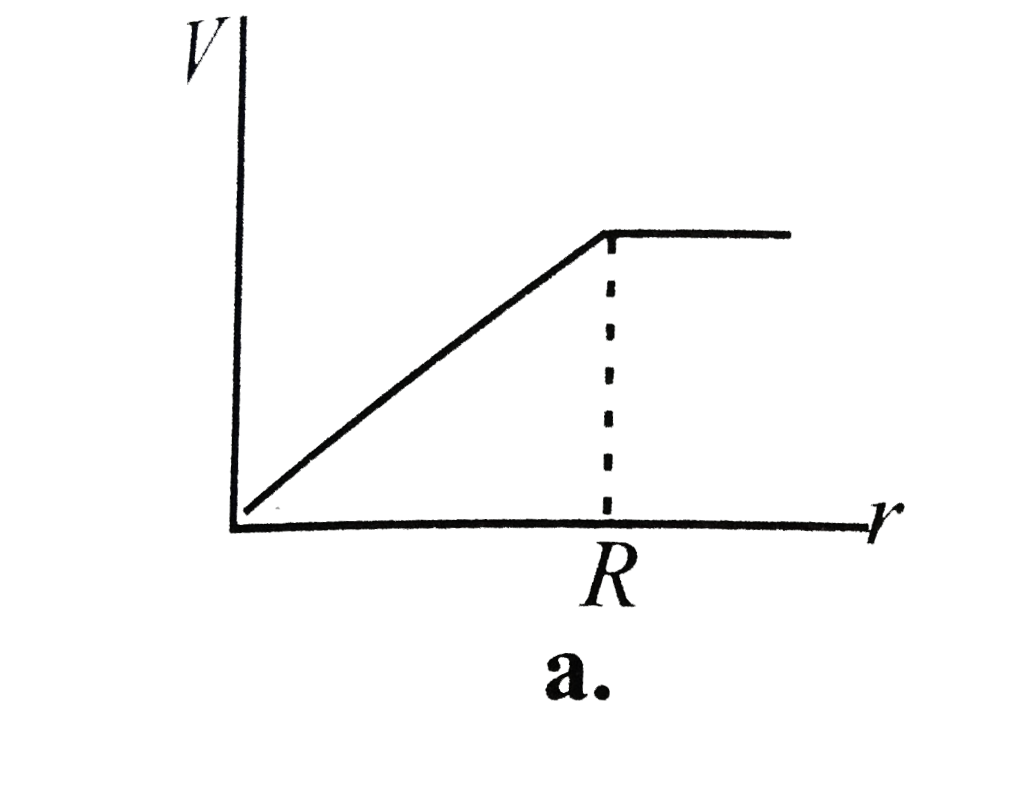
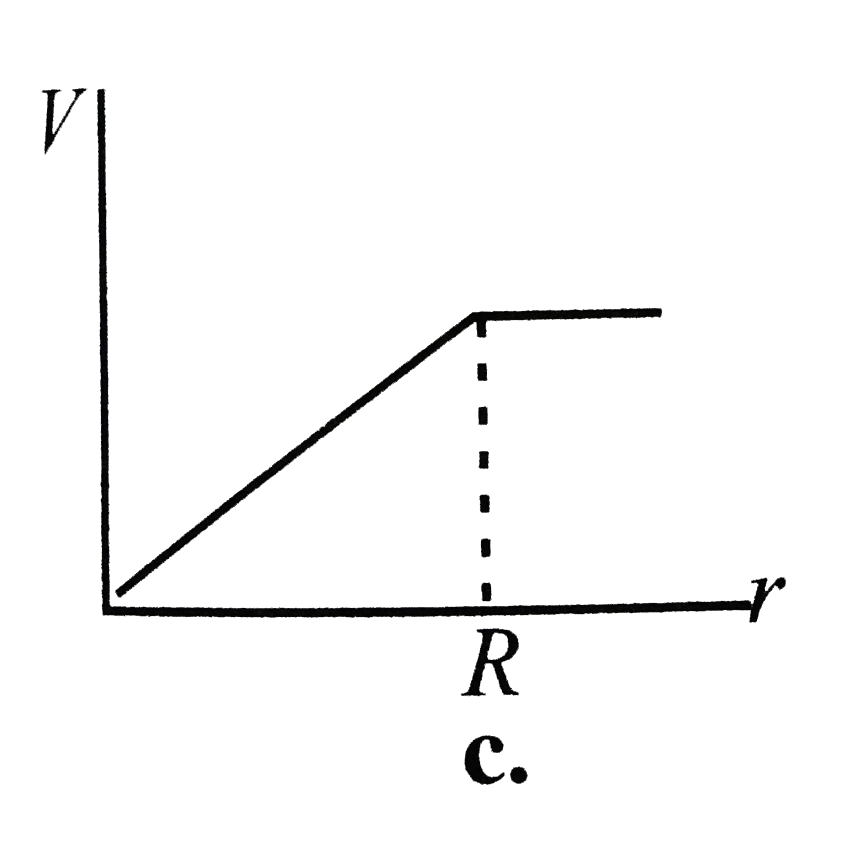

The correct Answer is:C
To solve the problem, we need to analyze the gravitational field created by a spherically symmetric mass distribution and how it affects the motion of a test mass in circular motion. The mass density is given as:
ρ={ρ0for r<R0for r>R
where ρ0 is a constant.
1. Understanding the Gravitational Force:
For a test mass m undergoing circular motion at a distance r from the center, the gravitational force provides the necessary centripetal force. The centripetal force is given by:
Fc=mv2r
where v is the speed of the test mass.
2. Calculating the Mass Inside Radius r:
The mass M enclosed within a radius r (for r<R) can be calculated using the volume and density:
M=ρ0⋅Volume=ρ0⋅43πr3
3. Using Newton's Law of Gravitation:
The gravitational force acting on the test mass m due to the enclosed mass M is given by:
Fg=GMmr2
where G is the gravitational constant.
4. Setting the Forces Equal:
For circular motion, we set the gravitational force equal to the centripetal force:
mv2r=GMmr2
Here, we can cancel m from both sides:
v2r=GMr2
5. Substituting for M:
Substitute M=43πr3ρ0 into the equation:
v2r=G(43πr3ρ0)r2
This simplifies to:
v2=43Gπρ0r
Thus, we find:
v∝√r
6. For r>R:
When r>R, the mass M enclosed is constant (equal to the total mass of the sphere):
M=43πR3ρ0
The gravitational force acting on the test mass is:
Fg=GMmr2
Setting the forces equal again:
mv2r=GMmr2
Canceling m gives:
v2r=G(43πR3ρ0)r2
This simplifies to:
v2=43GπR3ρ0⋅1r
Thus, we find:
v∝1√r
Final Result:
- For r<R: v∝√r
- For r>R: v∝1√r
For a test mass m undergoing circular motion at a distance r from the center, the gravitational force provides the necessary centripetal force. The centripetal force is given by:
Fc=mv2r
where v is the speed of the test mass.
The mass M enclosed within a radius r (for r<R) can be calculated using the volume and density:
M=ρ0⋅Volume=ρ0⋅43πr3
The gravitational force acting on the test mass m due to the enclosed mass M is given by:
Fg=GMmr2
where G is the gravitational constant.
For circular motion, we set the gravitational force equal to the centripetal force:
mv2r=GMmr2
Here, we can cancel m from both sides:
v2r=GMr2
Substitute M=43πr3ρ0 into the equation:
v2r=G(43πr3ρ0)r2
This simplifies to:
v2=43Gπρ0r
Thus, we find:
v∝√r
When r>R, the mass M enclosed is constant (equal to the total mass of the sphere):
M=43πR3ρ0
The gravitational force acting on the test mass is:
Fg=GMmr2
Setting the forces equal again:
mv2r=GMmr2
Canceling m gives:
v2r=G(43πR3ρ0)r2
This simplifies to:
v2=43GπR3ρ0⋅1r
Thus, we find:
v∝1√r
- For r<R: v∝√r
- For r>R: v∝1√r
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - MCQ_TYPE
4 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - AR_TYPE
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View Solution
Knowledge Check
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A12R√(1Gm)B√(Gm2R)C12√(GmR)D√(4GmR)Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B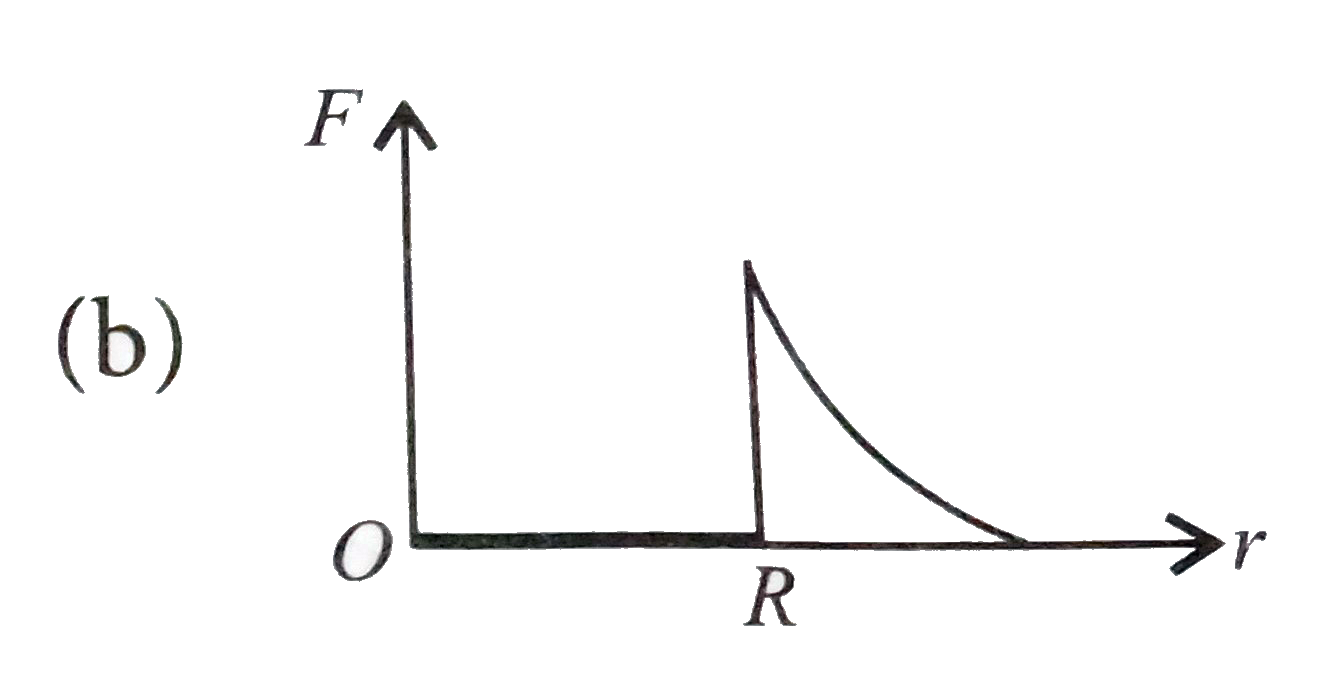 C
C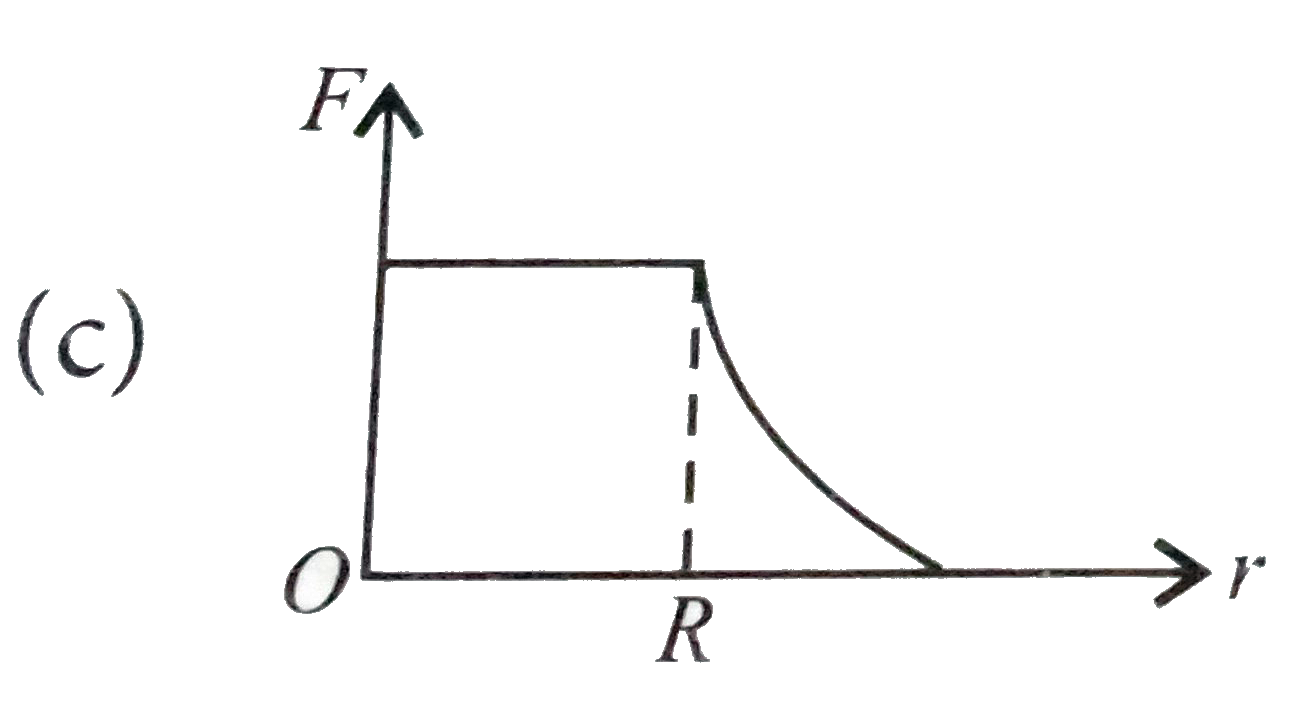 D
D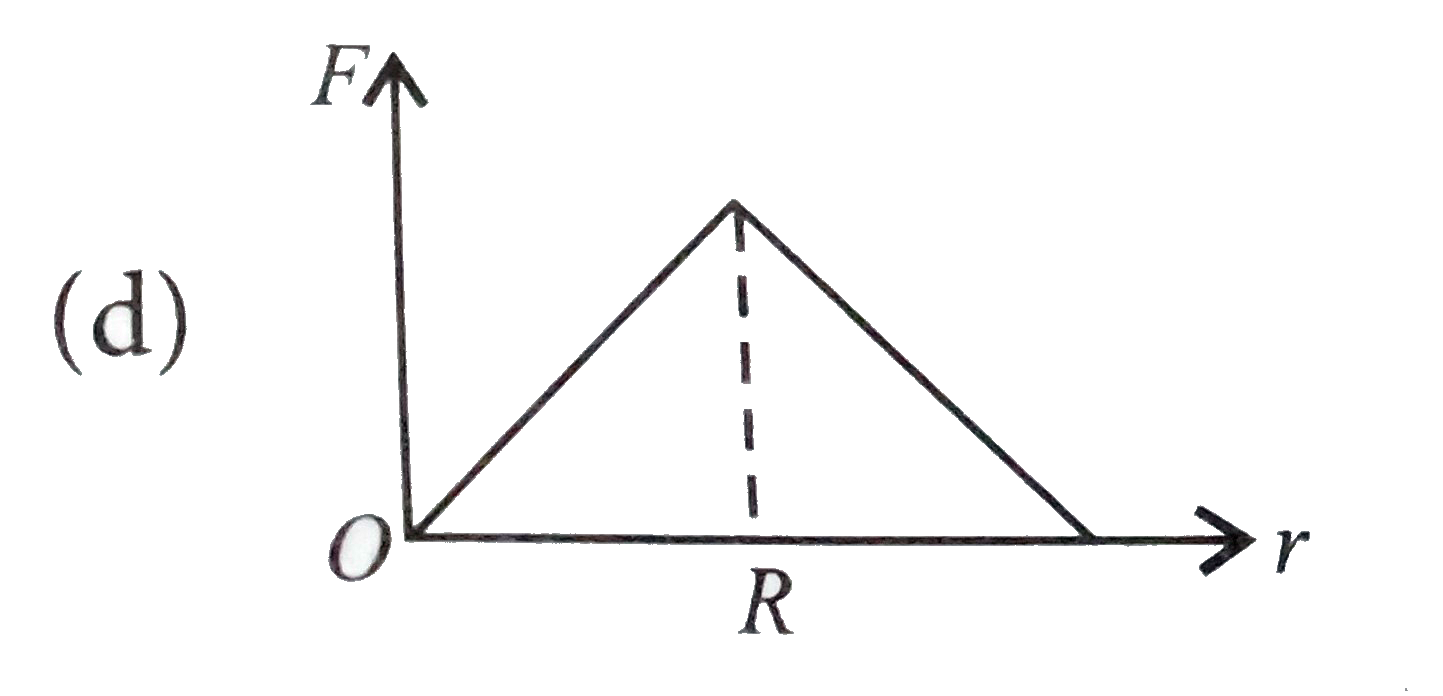
Three particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionFour particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionThe mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
View Solution
