Derive an expression for the height of capillary rise between two parrallel plates dipping in a liquid of density separated by a distance . The surface tension of the liquid is .
To derive the expression for the height of capillary rise between two parallel plates dipping in a liquid, we can follow these steps:
Step 1: Understand the Setup
We have two parallel plates separated by a distance d and dipping into a liquid with density σ. The surface tension of the liquid is T. We need to find the height h of the liquid column that rises between these plates due to capillary action.
Step 2: Identify Forces Acting on the Liquid Column
When the liquid rises between the plates, there are two main forces acting on it:
1. Upward Force due to Surface Tension: This force arises from the surface tension acting along the length of the plates.
2. Downward Force due to Weight of the Liquid Column: This force is the weight of the liquid column that has risen between the plates.
Step 3: Calculate the Upward Force due to Surface Tension
The total upward force FT due to surface tension can be calculated as:
FT=2T⋅L
where L is the length of the plates in contact with the liquid. The factor of 2 accounts for the surface tension acting on both sides of the plates.
Step 4: Calculate the Downward Force due to Weight
The weight W of the liquid column can be expressed as:
W=Volume×Density×g
The volume of the liquid column is given by A⋅h, where A is the cross-sectional area of the plates. Therefore, we have:
W=A⋅h⋅σ⋅g
Step 5: Set Up the Equilibrium Condition
At equilibrium, the upward force due to surface tension equals the downward weight of the liquid column:
FT=W
Substituting the expressions from Steps 3 and 4:
2T⋅L=A⋅h⋅σ⋅g
Step 6: Solve for Height h
Rearranging the equation to solve for h:
h=2T⋅LA⋅σ⋅g
Step 7: Relate Area to Plate Separation
The area A can be related to the distance d between the plates. If we assume that the plates are very close together, we can approximate A as d⋅L (where d is the separation between the plates). Thus:
h=2Tσg⋅Ld
Final Expression
The final expression for the height of capillary rise h between two parallel plates is:
h=2Tσg⋅Ld
We have two parallel plates separated by a distance d and dipping into a liquid with density σ. The surface tension of the liquid is T. We need to find the height h of the liquid column that rises between these plates due to capillary action.
When the liquid rises between the plates, there are two main forces acting on it:
1. Upward Force due to Surface Tension: This force arises from the surface tension acting along the length of the plates.
2. Downward Force due to Weight of the Liquid Column: This force is the weight of the liquid column that has risen between the plates.
The total upward force FT due to surface tension can be calculated as:
FT=2T⋅L
where L is the length of the plates in contact with the liquid. The factor of 2 accounts for the surface tension acting on both sides of the plates.
The weight W of the liquid column can be expressed as:
W=Volume×Density×g
The volume of the liquid column is given by A⋅h, where A is the cross-sectional area of the plates. Therefore, we have:
W=A⋅h⋅σ⋅g
At equilibrium, the upward force due to surface tension equals the downward weight of the liquid column:
FT=W
Substituting the expressions from Steps 3 and 4:
2T⋅L=A⋅h⋅σ⋅g
Rearranging the equation to solve for h:
h=2T⋅LA⋅σ⋅g
The area A can be related to the distance d between the plates. If we assume that the plates are very close together, we can approximate A as d⋅L (where d is the separation between the plates). Thus:
h=2Tσg⋅Ld
The final expression for the height of capillary rise h between two parallel plates is:
h=2Tσg⋅Ld
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
In a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -

View SolutionIt is said that a liquid rises or is depressed in a capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero ?
View Solution
Knowledge Check
When two capillary tubes of different diameters are dipped vertically, the rise of the liquids is
Asame in both the tubesBmore in tube of larger diameterCless in tube of smaller diameterDmore in the tube of smaller diameter
A drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionDerive an expression for the capacitance of a parallel plate capacitor in terms of the areas of the plates and the distance between them. Assume there is a vacuum in between the plates with the electric field between the plates E=σε0 (where the symbols have their usual meaning).
View SolutionWhat is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is ρ)
View SolutionDerive an expression for the angular frequency of small oscillation of the bob of a simple pendulum when it is immerased in a liquid of density ρ. Assume the density of the bob as σ and length of the string as l.
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View Solution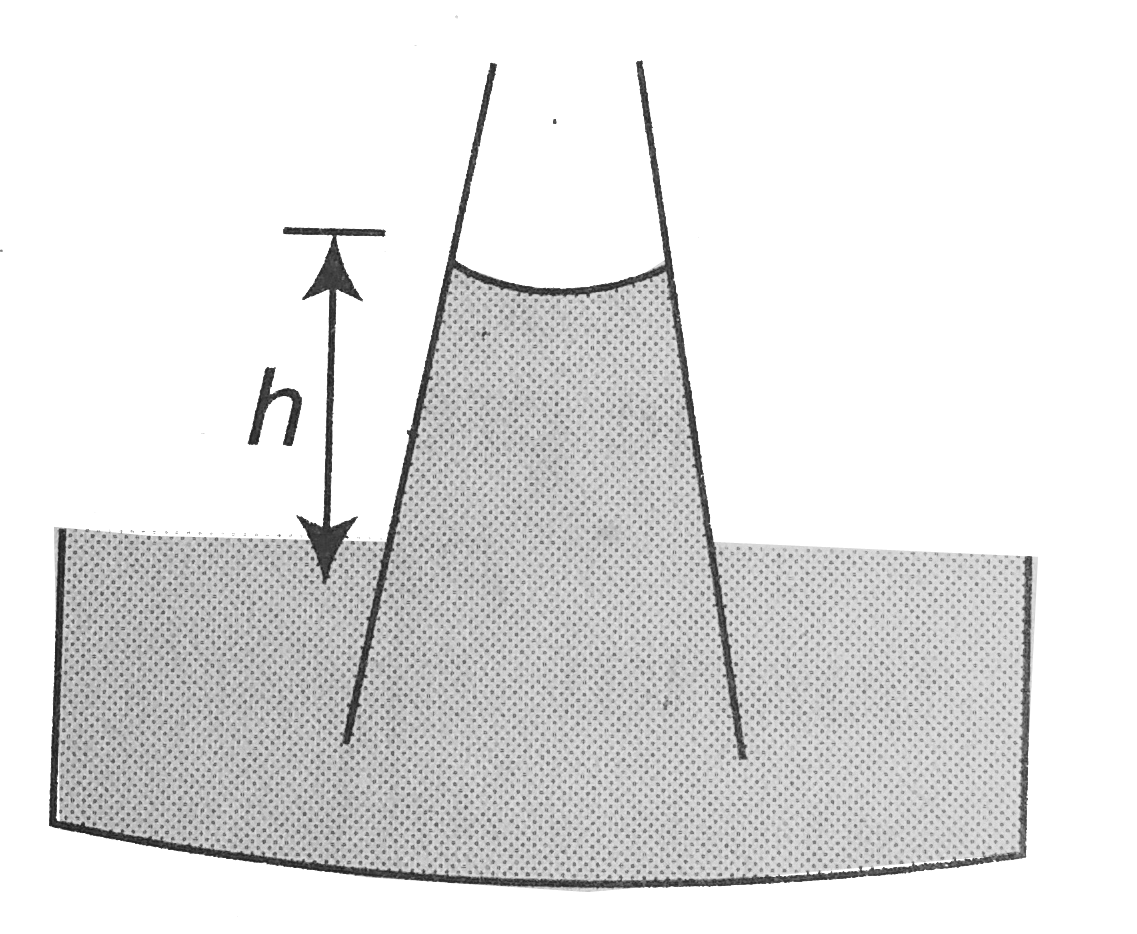
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View Solution
A container is partially filled with a liquid of density ρ2 A capillary tube of radius r is vertically inserted in this liquid. Now another liquid of density ρ1(ρ1<ρ2) is slowly poured in the container to a height h as shown. There is only denser liquid in the capillary tube. The rise of denser liquid in the capillary tube is also h. Assuming zero contact angle, the surface tension of heavier liquid is
View Solution
