Two skaters each of mass 50kg, approach each other along parallel paths separated by 3m. They have equal ad opposite velocities of 10m/s. The first skater carries a long light pole, 3m long, and the second skater grabs the end of it as he passes (assume frictionless ice).
a. Described quantitatively the motion of the skaters after they are connected by the pole.
b. By pulling on the skaters reduce their distance to 1m. What is their motion then?
c. Compare the KEs of the system in parts a. and b. where does the change come from?
To solve the problem step by step, we will break it down into parts a, b, and c as described in the question.
Part a: Motion of the Skaters After They Are Connected by the Pole
1. Initial Setup:
- Each skater has a mass m=50kg.
- They are moving towards each other with velocities v1=10m/s and v2=−10m/s (opposite directions).
- The distance between them is d=3m.
- When they grab the pole, they will start rotating around their center of mass.
2. Finding the Center of Mass (CM):
- The center of mass of the system can be found at a distance of 1.5m from each skater since they are of equal mass and separated by 3m.
3. Conservation of Angular Momentum:
- The initial angular momentum Li is given by:
Li=m⋅v⋅r=50⋅10⋅1.5=750kg m2/s
- After they are connected by the pole, they will rotate around the center of mass.
4. Calculating Angular Velocity:
- The moment of inertia I for both skaters about the center of mass is:
I=2⋅m⋅r2=2⋅50⋅(1.5)2=225kg m2
- Using conservation of angular momentum:
Lf=I⋅ω
750=225⋅ω⟹ω=750225=3.33rad/s
Part b: Reducing Their Distance to 1m
1. New Setup:
- The distance between the skaters is now d=1m.
- The radius r from the center of mass to each skater is now 0.5m.
2. Conservation of Angular Momentum Again:
- The initial angular momentum remains the same:
Li=750kg m2/s
3. New Moment of Inertia:
- The new moment of inertia I′ is:
I′=2⋅m⋅(0.5)2=2⋅50⋅0.25=25kg m2
4. Calculating New Angular Velocity:
- Using conservation of angular momentum:
750=25⋅ω′⟹ω′=75025=30rad/s
Part c: Comparing Kinetic Energies
1. Kinetic Energy in Part a:
- The kinetic energy KEa when they are 3m apart:
KEa=2⋅12mv2=2⋅12⋅50⋅(10)2=5000J
2. Kinetic Energy in Part b:
- The kinetic energy KEb when they are 1m apart:
KEb=2⋅12m(v′)2=2⋅12⋅50⋅(30)2=22500J
3. Comparison:
- The kinetic energy increases from 5000J to 22500J.
- The change in kinetic energy comes from the work done by the skaters as they pull on each other to reduce the distance.
- Each skater has a mass m=50kg.
- They are moving towards each other with velocities v1=10m/s and v2=−10m/s (opposite directions).
- The distance between them is d=3m.
- When they grab the pole, they will start rotating around their center of mass.
- The center of mass of the system can be found at a distance of 1.5m from each skater since they are of equal mass and separated by 3m.
- The initial angular momentum Li is given by:
Li=m⋅v⋅r=50⋅10⋅1.5=750kg m2/s
- After they are connected by the pole, they will rotate around the center of mass.
- The moment of inertia I for both skaters about the center of mass is:
I=2⋅m⋅r2=2⋅50⋅(1.5)2=225kg m2
- Using conservation of angular momentum:
Lf=I⋅ω
750=225⋅ω⟹ω=750225=3.33rad/s
- The distance between the skaters is now d=1m.
- The radius r from the center of mass to each skater is now 0.5m.
- The initial angular momentum remains the same:
Li=750kg m2/s
- The new moment of inertia I′ is:
I′=2⋅m⋅(0.5)2=2⋅50⋅0.25=25kg m2
- Using conservation of angular momentum:
750=25⋅ω′⟹ω′=75025=30rad/s
- The kinetic energy KEa when they are 3m apart:
KEa=2⋅12mv2=2⋅12⋅50⋅(10)2=5000J
- The kinetic energy KEb when they are 1m apart:
KEb=2⋅12m(v′)2=2⋅12⋅50⋅(30)2=22500J
- The kinetic energy increases from 5000J to 22500J.
- The change in kinetic energy comes from the work done by the skaters as they pull on each other to reduce the distance.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
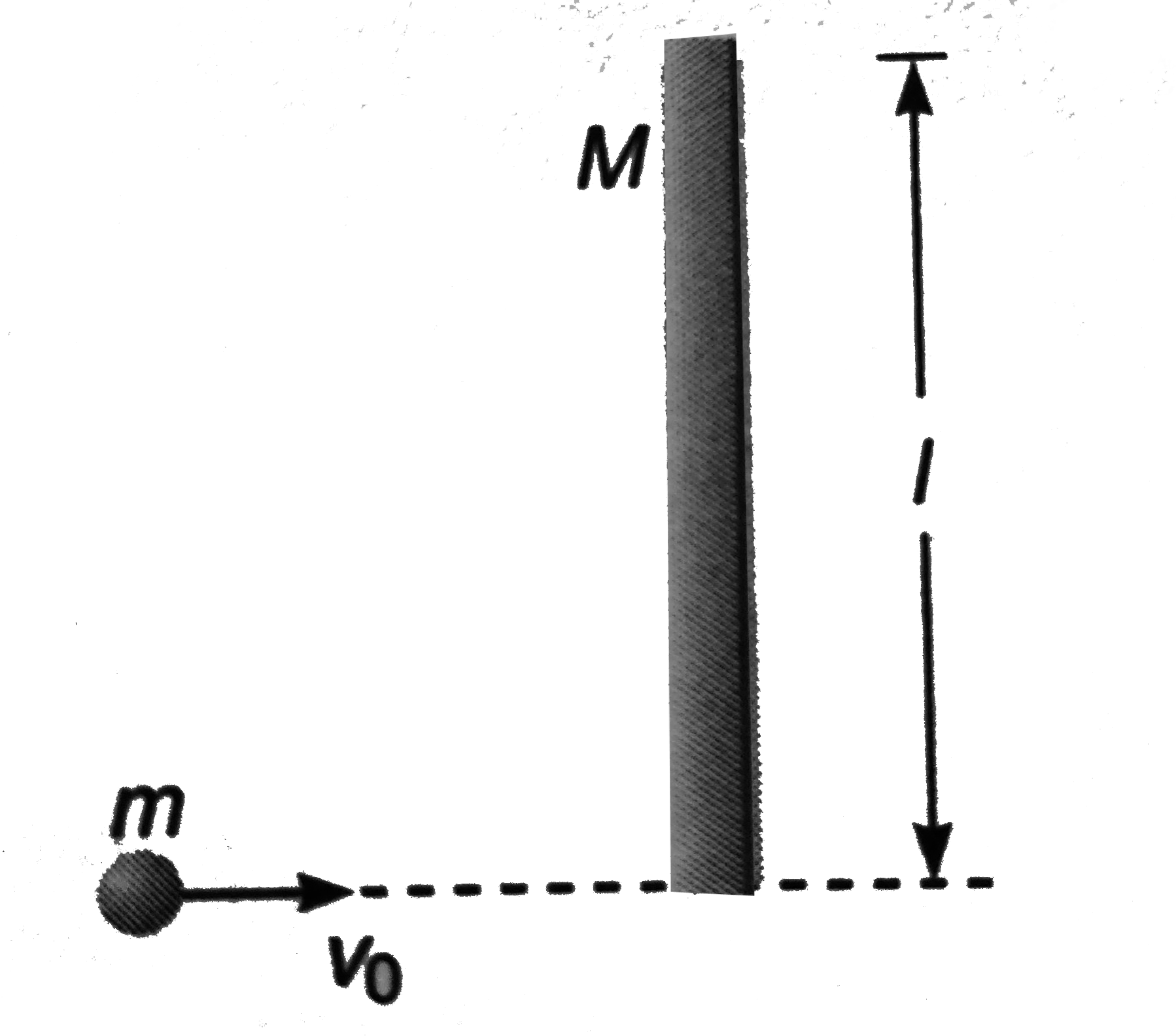
A boy mass m runs on ice with velocity v and steps on the end of a plank of length l and mass M which is perpendicular to his path.
(a). Describe quantitatively the motion of the system after the boy is on the plank. Neglect friction with the ice.
(b). One point on the plank is at rest immediately after the collision. Where is it?
View SolutionTwo skaters have weight in the ratio 4:5 and are 9m apart, on a smooth frictionless surface. They pull on a rope stretched between them. The ratio of the distance covered by them when they meet each other will be
View Solution
Knowledge Check
Two trains, each 50 m long are travelling in opposite direction with velocity 10 m/s and 15 m/s. The time of crossing is
A2sB4sC2√3sD4√3 sTwo stars each of mass M and radius R are approaching each other for a head-on collision. They start approaching each other when their separation is r>>R. If their speed at this separation are negligible, the speed v with which they collide would be
Av=√GM(1R−1r)Bv=√GM(12R−1r)Cv=√GM(1R+1r)Dv=√GM(12R+1r)
Two ice skaters A and B approach each other at right angles. A has mass 30 kg and velocity 1 mis and B has a mass of 20 kg and velocity 2 m/s. They meet and stick together. The final velocity of couple is :
View SolutionTwo particles of masses m and 3m approach each other with different velocities. After collision, the particle of mass m has velocity →v in their centre of mass frame. Velocity of particle of mass 3m in the centre of mass frame is
View SolutionTwo objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?

View SolutionTwo skaters A & B of mass M and 2M are standing together on a frictionless ice surface. They push each other apart. The skater B moves away from A with a speed of 2 m/s relative to ice. The separation between the two skaters after 5 seconds will be
View SolutionTwo cars move in the same direction along parallel roads. One of them is a 200m, long travelling with a velocity of 20m/s. The second one is 800m long travelling with a velocity of 7.5m/s. How long will it take for the first car to overtake the second car?
View SolutionTwo identical thin bar magnets, each of length L and pole strength m are placed at right angles to each other, with the N pole of one touching the S-pole of the other. Find the magnetic moment of the system.
View Solution
