A cannon and a supply of cannon balls are inside a sealed rail road car. The cannon fires to the right, the car recoils to the left. The canon balls remain in the car after hitting the far wall. Show that no matter how the cannon balls are fired, the rail road car cannot travel more than L. assuming it starts from rest.

Initially, the whole system is at rest, so vCM=0. As there is no external force acting on the system→vCM=constant =0. So position of centre of mass of system remains fixed.
xCM=mx1+Mx2m+M…………i
where in is mass of the cannon balls and M that of the (car + cannon) system.
As△xCM=0 therefore
m△x1+m△x2=0.....ii
As cannon balls cannot leave the car, so maximum displacement of the balls relative to the car is L and in doing so the car will shift a distance △x2=D(say) relative to the ground, opposite to the displacement of the balls, then the displacement of balls relative to ground will be
△x1=L−D.........iii
Substituting the value of △x1 from eqn iii in eqn ii we get
m(L−D)−MD=0
⇒D=mLM+m=L1+Mm
⇒D<L
i.e. rail road car cannot travel more than L,
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Exercise 1.2
Explore 23 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Exercise 1.3
Explore 24 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Solved Examples
Explore 13 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A ball hangs from a string inside a rail road car moving along a straight track. The string is observed to be inclined towards the rear of the car making a constant small angle with the vertical. It shows that the car is
View SolutionA cannon-ball is fired with a speed 50m/sec with respect to ground from one end of a stationary railroad car which rests on a smooth track. The ball collides with opposite wall and stops. How much distance did the railroad car cover just before the collision? Given that the ratio of the mass of the ball to that of the railroad car is 1/99 and the length of the car is 50m

View Solution
Knowledge Check
y=−5t2+2t+20
x=2t
A cannonball is shot out of a cannon at a 45∘ angle with an approxiate speed of 283m/s. The cannon from which the ball was fired sits on the edges of a cliff, and its height above the ground is 20 meters. The equations given above represent the cannonball's height above the ground(y) and its horizontal distance (x) from the face of the cliff, t seconds after the ball was fired, where t≥0. How many seconds after the ball was fired does its vertical height above the ground equal its horizontal distance from the cliff?A1B2C3D4
Two 20kg cannon balls are chained together and fired horizontally with a velocity of 200m/s from the top of a 30m wall. The chain breaks during the flight of the cannon balls and one of them strikes the ground at t=2s, at a distance of 250m from the foot fo the wall, and 5m to the right of line of fire determine the position of the other cannon ball at that instant Neglect the resistance of air.

View SolutionA car starts from rest on a half kilometer long bridge. The coefficiet of friction between the tyre and the road is 1.0. Show that one cannot drive thrugh the bridge in less than 10 s.
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration a1anda2 respectively. Show that v=√a1a2t.
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration a1anda2 respectively. Show that v=√a1a2t.
View SolutionA car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in the figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100 m/s with respect to the car at an angle 30∘ with the horizontal.

The first cannon ball hits the stationary carriage after a time t0 and sticks to it. Determine t0. (in sec)
View SolutionCannon A is located on a plain a distance L from a wall of height H. On top of this wall is an idential cannon (cannon B). Ignore air resistance throughout this problem.
Also ignore the size of the cannons relative to LandH. The two groups of gunners aim the cannons directly at each other. They fire at each other simultaneously, with equal muzzle speed v0
What is the velue of v0 for which the two cannon balls collide just as they hit the ground ?
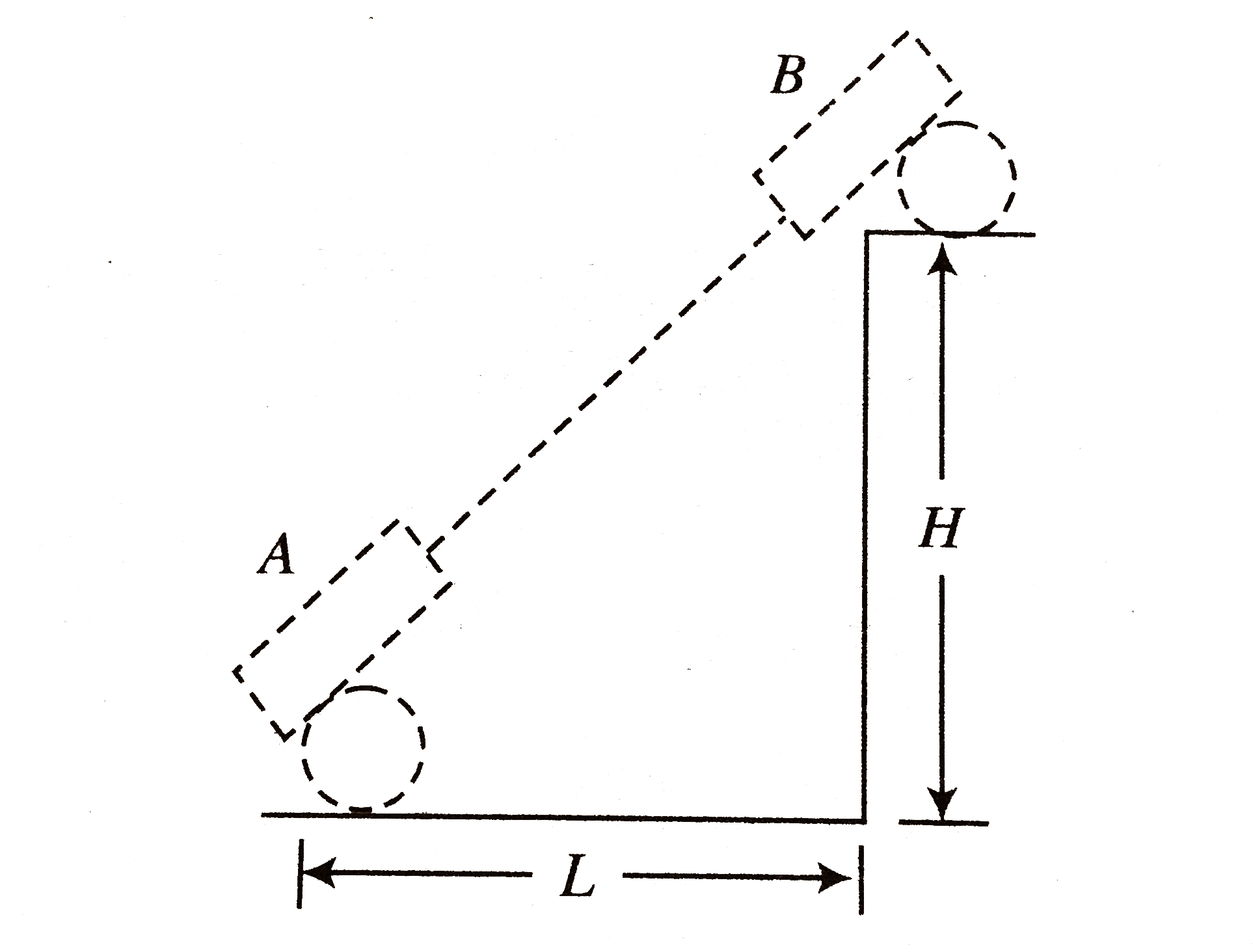 .
.
View SolutionA heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 60cms−1 on the string when the car is at rest and 62cms−1 when the car accelerates on a horizontal road. Find the acceleration of the car. Take g=10ms−2
View Solution

