Figure shows a flat car of mass M on a frictionless road. A small massless wedge is fitted on it as shown. A small ball of mass m is released from the top of the wedge, it slides over it and falls in the hole at distance l from the initial position of the ball. Find the distance the flat car moves till the ball gets into the hole.

When the bell falls into the hole, with respect to the flat car, the bail travels a horizontal distance l. During this motion, to conserve momentum and to maintain the position of centre of mass, the car moves towards left, say by a distance x. Thus, the total distance travelled by the ball towards right is (l−x). As centre of mass remains at rest, the change in mass moments of the two (ball and car) about any point must be equal to zero. Hence
m(l−x)=MΞmpliesm=mlM+m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
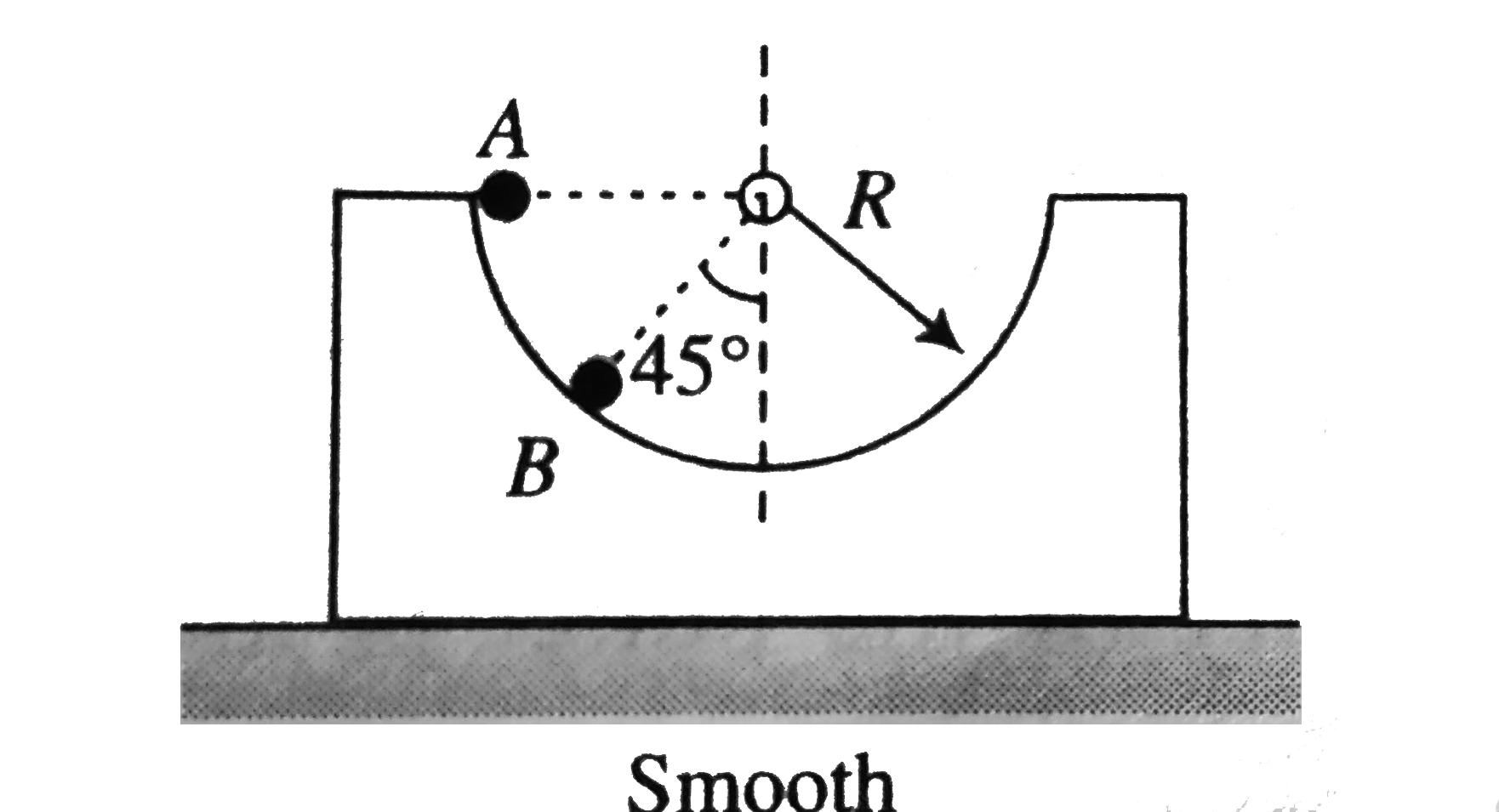
A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
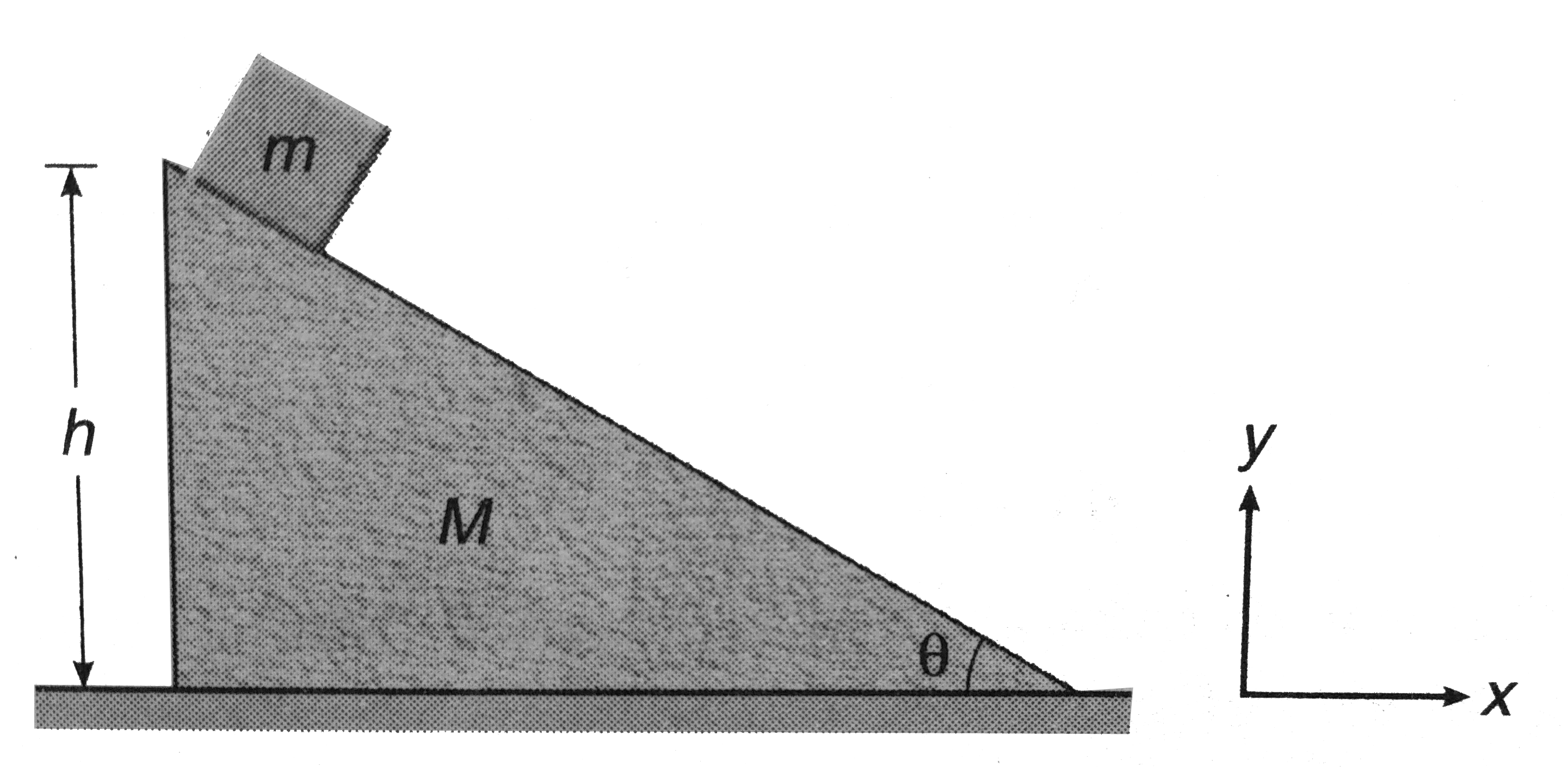
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
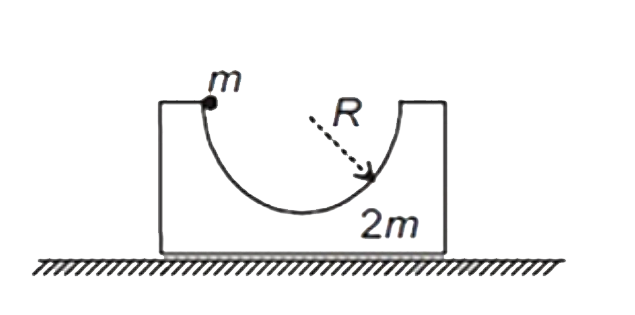
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is

View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small ball of mass m is released in a smooth circular tube as shown in figure. The minimum height h such that bead can complete the circle is
View SolutionA ball of mass m is projected from a point P on the ground as shown in the figure. It hits a fixed vertical wall at a distance l from P. Choose the most appropriate option :

View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

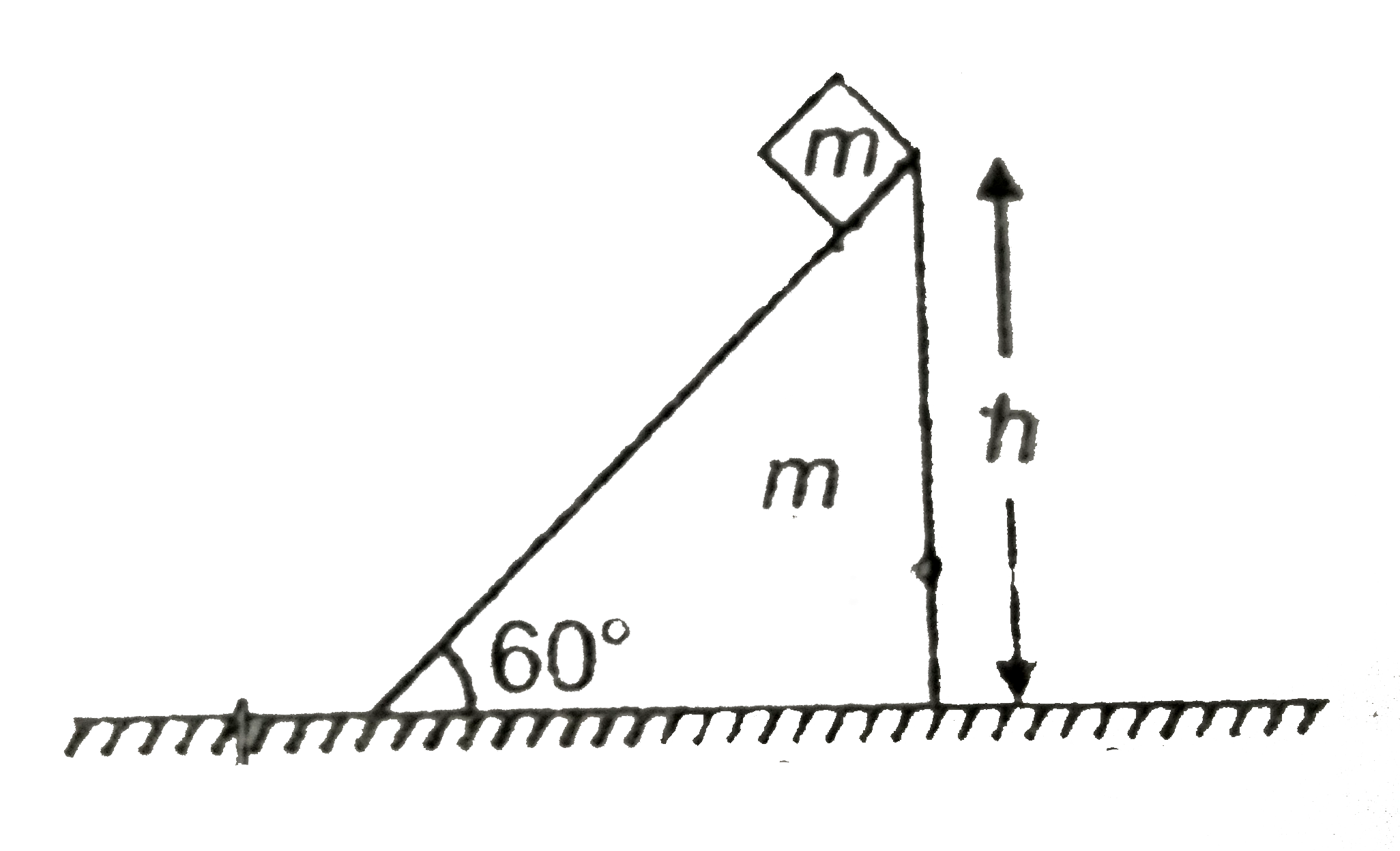
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA ball of mass mis released from the top of an inclined plane of inclination θ as shown. It strikes a rigid surface at at a distance 3l4 from top elastically. Impulse imparted to ball by the rigid surface is
View Solution
