Two small discs of masses m1 and m2 are connected by a weightless spring resting on a smooth horizontal plance. The discs are set in motion with initial velocities v1andv2 whose directions are mutually perpendicular and in the same horizontal plane. Find the total energy E of the system with reference to the frame fixed to the centre of mass.
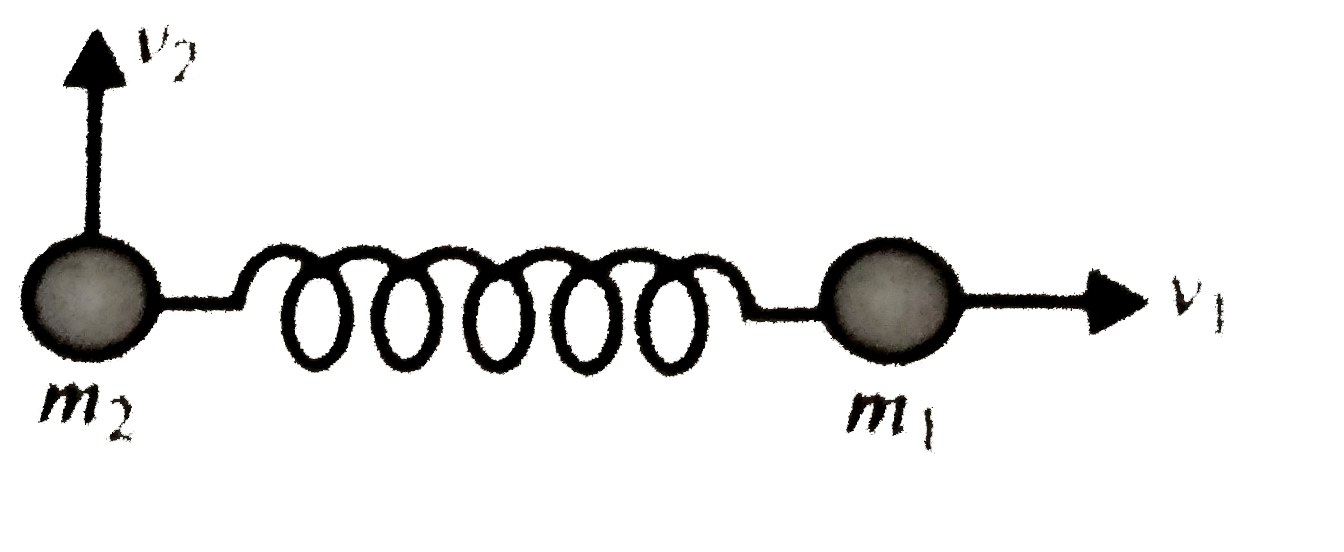
Let →vcm be the velocity of the centre of mass. Velcoity of m1 relative to thecentre of mas is (→v1−→vcm) and that of m2 relative to the centre of mass is (→v2−→v1)
Velocity of centre of mass →vcm=m1→v1m2→v2m1+m2
(→v1−→vcm)=m2m1+m2(→v1−→v2)
Hence |→v1−→vcm|=m2m1+m2(v21+v22)1/2
and →v2−→vcm=m1m1+m2(→v2−→v1)
Hence |→v2−→vcm|=m1m1+m2(v21+v22)1/2
total energy with respect to the centre of mass,
E=12m1|→v1−→vcm|212m1|→v2−→vcm|2
=12(m1m2m1+m2)(v21+v22)
where μ=m1m2m1+m2 is called reduced mass.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
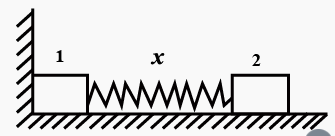
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
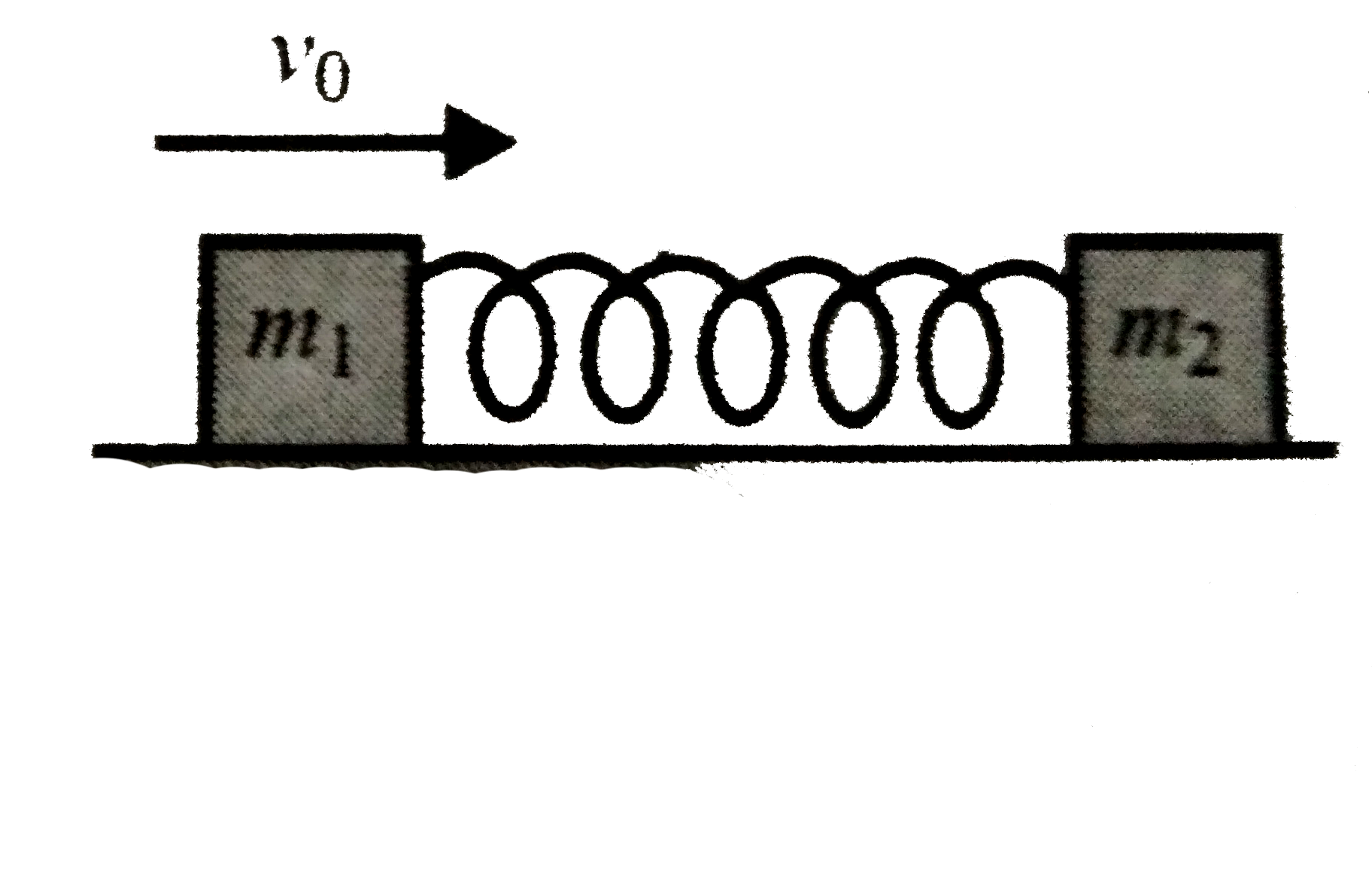
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
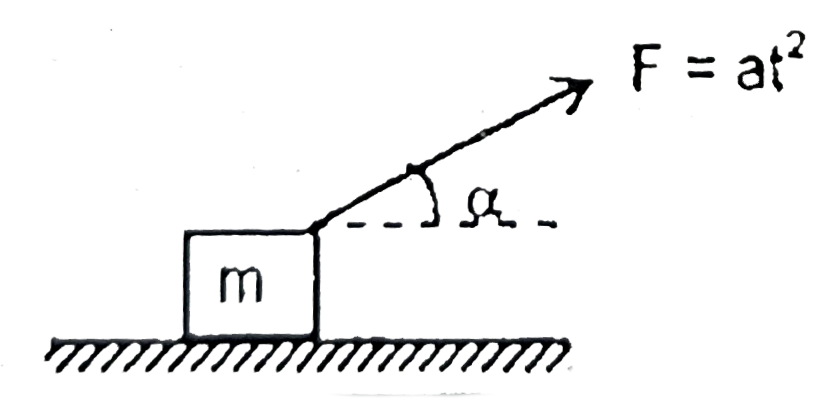
View SolutionAt t=0, a force F=at2 is applied to a small body of mass m at an angle α resting on a smooth horizontal plane
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo masses, m1 and m2 , are moving with velocities v1 and v2. Find their total kinetic energy in the reference frame of centre of mass.
View SolutionChoose the correct option:
Two bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The velocity of the centre of mass of the system when bar 1 breaks off the wall is

View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

View Solution
