An amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is μs and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is T=(4π2μsR/g)1/2
b. Obtain a numerical value for T taking R=4.00m and μs=0.400 . How many revolations per minute does the cylinder make?
c. If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d. If instead the cylinder rate revolution is made to be somewhat smaller what happens to the magnitude and what happens to the motion of the person ?
a. N=mv2R,f−mg=0,f=μsN,v=2×πRT
Solving we get T=√4π2Rμsg
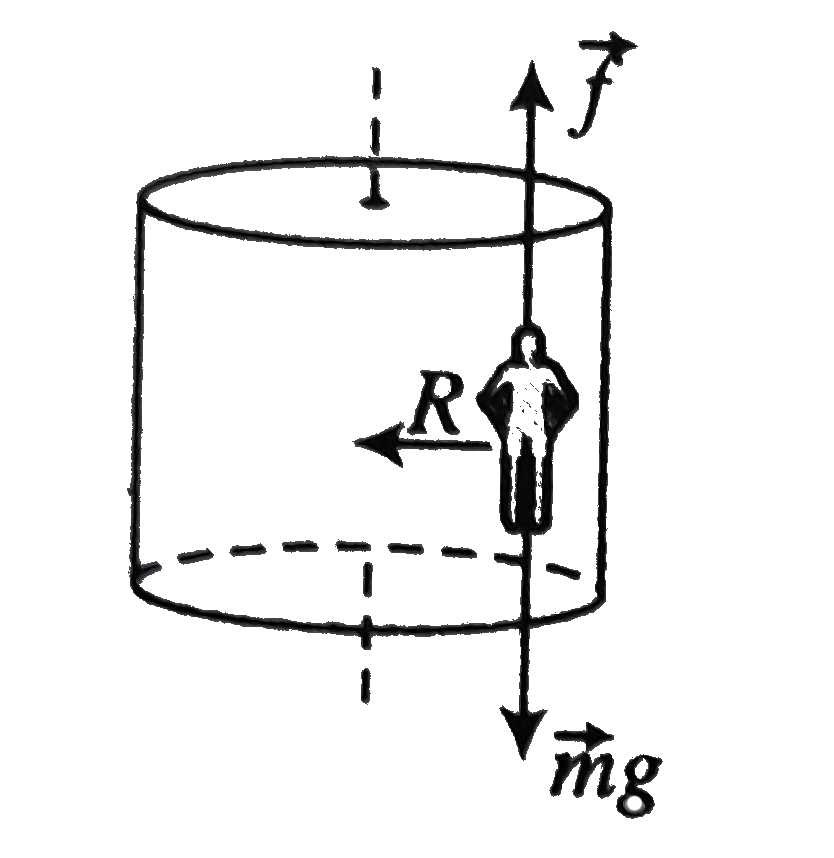
b. T=0.8πs
revmin=600.8π=75πrev−1min
c. The gravitational and the friction force remain constant . The normal force increases .The person remains in motion with the wall .
d. The gravitational force remain constant . The normal and the frictional forces decrease . THe person slides relative to the wall and downward into the pit
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
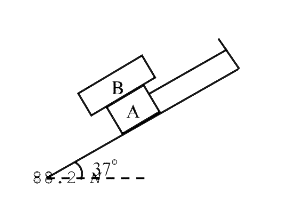
Find μs between A and B.
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solutionif the earth is treated as a sphere of radius R and mass M, Its angular momentum about the axis of its rotation with period T, is
View SolutionThe relation between length L and radius R of the cylinder , if its moment of inertia about its axis is equal to that about the equatorial axis, will be
View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View Solution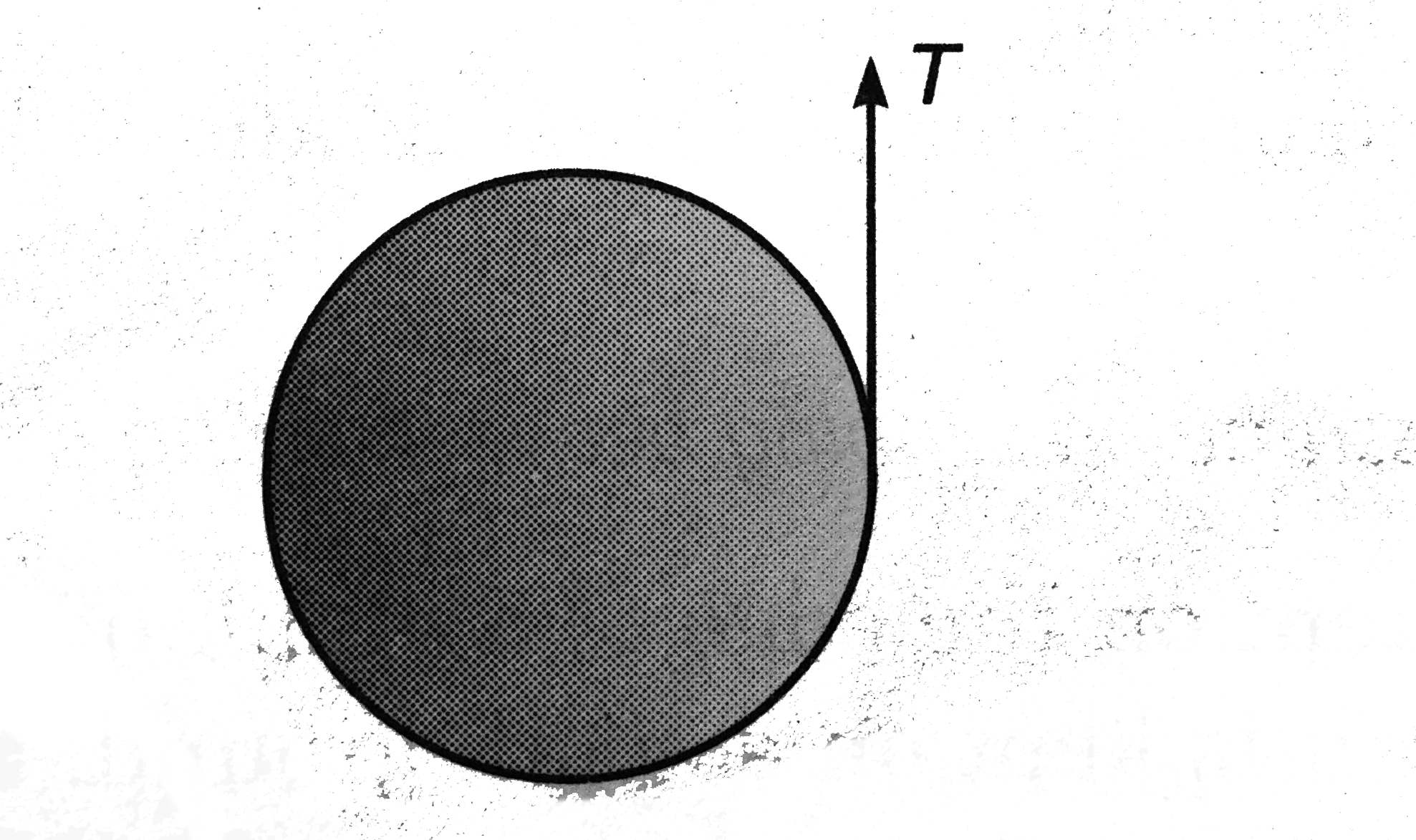
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View SolutionA sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is 4π r3 (b) 83π r3 (c) 2π r3 (d) 8π r3
View SolutionWhat will happen to the inductance of a solenoid
a. when the number of turns and the length are double keeping the area of cross section same?
b. when the air inside the solenoid is replaced by iron of relative permeability μr?
View SolutionA cylinder is filled with a liquid of refractive index μ. The radius of the cylinder is decreasing at a constant rate K. The volume of the liquid inside the container remains constant at V. The observer and the object O are in a state of rest at a distance L from each other. When radius of cylinder is r the apparent velocity of the object as seen by the observer is

View Solution
