The silicate anion in the mineral kinoite is a chain of three SiO4 tetrahedra, that share corners with adjacent tetrahedra. The charge pof silicate anion is
−4
−8
−6
−2
The correct Answer is:B
To determine the charge of the silicate anion in the mineral kinoite, we can follow these steps:
Step 1: Understand the Structure of the Silicate Anion
The silicate anion in kinoite consists of three SiO4 tetrahedra that share corners with each other. Each SiO4 tetrahedron has one silicon atom (Si) and four oxygen atoms (O).
Step 2: Determine the Total Number of Silicon and Oxygen Atoms
In the chain of three SiO4 tetrahedra:
- There are 3 silicon atoms (Si).
- Each tetrahedron has 4 oxygen atoms, but since they share corners, we need to calculate the total number of unique oxygen atoms.
Step 3: Calculate the Unique Oxygen Atoms
When three SiO4 tetrahedra are connected:
- The first tetrahedron contributes 4 oxygen atoms.
- The second tetrahedron shares one oxygen with the first, contributing 3 additional unique oxygen atoms.
- The third tetrahedron shares one oxygen with the second, contributing 3 additional unique oxygen atoms.
Thus, the total number of unique oxygen atoms is:
- 4 (from the first tetrahedron) + 3 (from the second) + 3 (from the third) = 10 oxygen atoms.
Step 4: Write the Formula for the Silicate Anion
The formula for the silicate anion in kinoite can be represented as Si3O10.
Step 5: Determine the Charge of the Silicate Anion
Each silicon atom has a +4 charge, and each oxygen atom has a -2 charge. Therefore:
- Total charge from silicon: 3 Si x +4 = +12
- Total charge from oxygen: 10 O x -2 = -20
Now, we can calculate the overall charge of the silicate anion:
Overall charge = Total charge from silicon + Total charge from oxygen
Overall charge = +12 - 20 = -8
Conclusion
The charge of the silicate anion in the mineral kinoite is -8.
Final Answer
The charge of the silicate anion in the mineral kinoite is -8.
---
The silicate anion in kinoite consists of three SiO4 tetrahedra that share corners with each other. Each SiO4 tetrahedron has one silicon atom (Si) and four oxygen atoms (O).
In the chain of three SiO4 tetrahedra:
- There are 3 silicon atoms (Si).
- Each tetrahedron has 4 oxygen atoms, but since they share corners, we need to calculate the total number of unique oxygen atoms.
When three SiO4 tetrahedra are connected:
- The first tetrahedron contributes 4 oxygen atoms.
- The second tetrahedron shares one oxygen with the first, contributing 3 additional unique oxygen atoms.
- The third tetrahedron shares one oxygen with the second, contributing 3 additional unique oxygen atoms.
- 4 (from the first tetrahedron) + 3 (from the second) + 3 (from the third) = 10 oxygen atoms.
The formula for the silicate anion in kinoite can be represented as Si3O10.
Each silicon atom has a +4 charge, and each oxygen atom has a -2 charge. Therefore:
- Total charge from silicon: 3 Si x +4 = +12
- Total charge from oxygen: 10 O x -2 = -20
Overall charge = Total charge from silicon + Total charge from oxygen
Overall charge = +12 - 20 = -8
The charge of the silicate anion in the mineral kinoite is -8.
The charge of the silicate anion in the mineral kinoite is -8.
Topper's Solved these Questions
- p-BLOCK ELEMENTSBOOK - VK JAISWAL ENGLISHCHAPTER - p-BLOCK ELEMENTSEXERCISE - LEVEL 2
97 Videos
- p-BLOCK ELEMENTSBOOK - VK JAISWAL ENGLISHCHAPTER - p-BLOCK ELEMENTSEXERCISE - LEVEL 3 (PASSAGE TYPE)
17 Videos
- METALLURGYBOOK - VK JAISWAL ENGLISHCHAPTER - METALLURGYEXERCISE - ASSERTION-REASON TYPE QUESTIONS
29 Videos
- PERIODIC PROPERTIESBOOK - VK JAISWAL ENGLISHCHAPTER - PERIODIC PROPERTIESEXERCISE - MATCH THE COLUMN
11 Videos
Similar Questions
The silicate anion in the mineral kinoite is a chain of three SiO4 tetrahedra, that share corners with adjacent tetrahedra. The charge of silicate anion is
View SolutionThe silicate anion in the mineral Kionite is a chain of three SiO4 tetrahedra that share corners with adjacent tetrahedra. The mineral also contains Ca2+ ions, Cu2+ ions, and water molecules in a 1:1:1 ration.
(a) Give the formula and charge of the silicate anion.
(b) GIve the complete formula for the mineral.
View SolutionThe silicate ion in the mineral kinoite is a chain of three SiO4−4 tetrahedral that share corners with adjacent tetrahedral. The mineral also contains Ca2+ ions, Cu2+ ions and water molecules in 1:1:1 ratio. The mineral is represented as
View SolutionThe silicate ion in the mineral kinoite is a chain of three SiO4−4 tetrahedral that share corners with adjacent tetrahedral. The mineral also contains Ca2+ ions, Cu2+ ions and water molecules in 1:1:1 ratio. The mineral is represented as
View SolutionThe silicate ion in the mineral kinoite is a chain of three SiO4−4 tetrahedral that share corners with adjacent tetrahedral. The mineral also contains Ca2+ ions, Cu2+ ions and water molecules in 1:1:1 ratio. The mineral is represented as
View SolutionThe general formula of tetrahedra silicates arranged in chain pattern is :
View SolutionWhich of the following minerals corners shared per silicate unit ?
View SolutionThe name 'silica' covers an entire group of minerals which have the
general formula SiO2 the most tetrahedra arranged in spirals . The spirals can turn in a clockwise or anti-clockwise direction - a feature that results in these being two mirror images optically active,
varieties of quartz.
The following pictures represent various silicate anions.
Their formulae are respectively :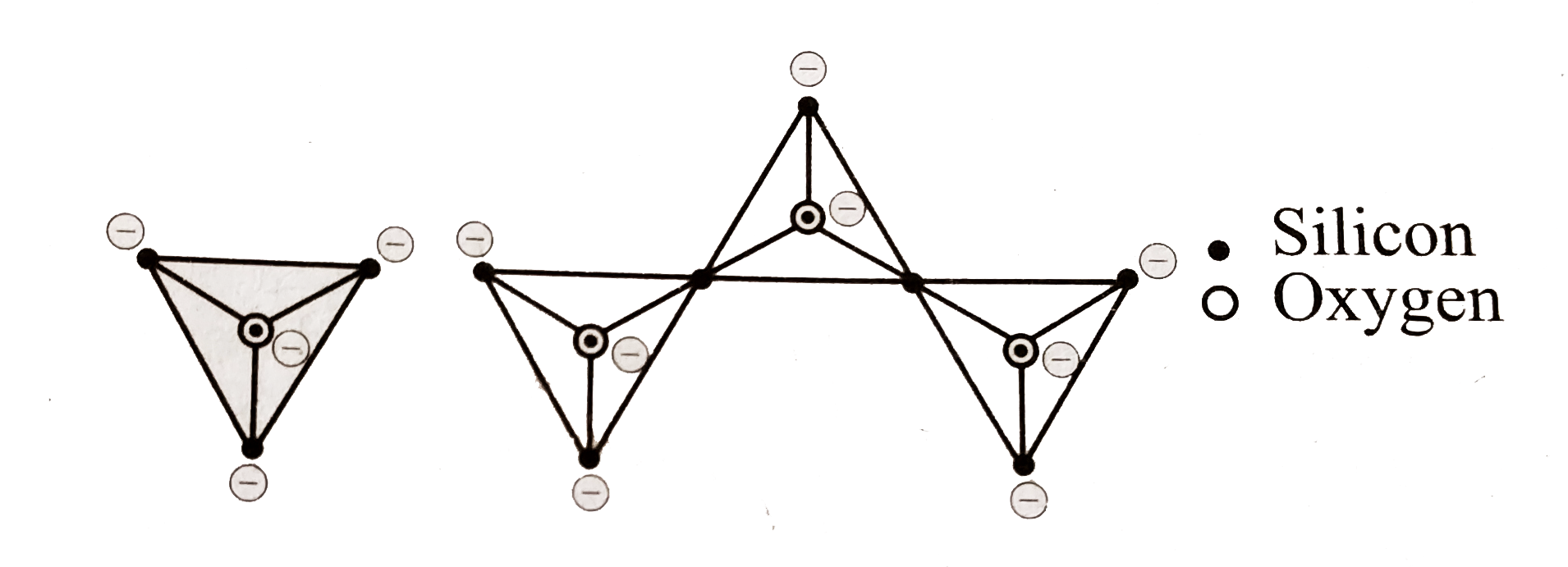 .
.
View SolutionThe name 'silica' covers an entire group of minerals which have the general formula SiO2 the most tetrahedra arranged in spirals . The spirals can turn in a clockwise or anti-clockwise direction - a feature that results in these being two mirror images optically active,
varieties of quartz.
Si3O6−9 (having three tetrahedra ) is represented as :
View SolutionThe name of the structure of silicates in which three oxygen atoms of [SiO4]4− are shared is
View Solution
