A straight line passes through the points (2,4) and (5,-2).Taking 1 cm=1 unit, mark these points on a graph paper and draw the straight line through these points. If points (m,-4) and (3,n) lie on the line drawn, find the values of m and n.
The correct Answer is:2
Step by step video & text solution for A straight line passes through the points (2,4) and (5,-2).Taking 1 cm=1 unit, mark these points on a graph paper and draw the straight line through these points. If points (m,-4) and (3,n) lie on the line drawn, find the values of m and n. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
On a graph paper, mark the points A(-1,-1) and B(2,5) Draw a straight line passing through A and B. If points (m,4) and (0.5,n ) lie on this line , use graphical method of finding the values of m and n .
View SolutionPlot the points (3, 5)and (−1, 3) on a graph paper and verify that the straight line passing through these points also passes through the point (1, 4).
View Solutionfind the gradient and intercepts on the axes of the straight line passing through the point (1,−3) and (4,5).
View SolutionGraph the line passing through the point P and having slope m.
P=(2,4),m=−3
View SolutionFind the equation of a line passing through the points (2,5) and (−3,1).
View SolutionDraw the graph (straight line) given by equation x−3y=18. If the straight line drawn passes through the points (m,-5) and (6,n), find the values of m and n.
View SolutionIf the points A(3, 5)and B(1, 4) lie on the graph of the line ax+by=7, find the values of a and b
View SolutionWhat will be the value of m and c if the straight line y=mx+c passes through the points (3, -4) and (-1, 2) ?
View SolutionShow that the three points (5, 1), (1, -1) and (11, 4) lie on a straight line. Further find
the slope of the line.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
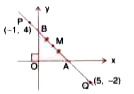
The co-ordinates of A and B.
View Solution
