The graph of y=f''(x) for a function f is shown.
Number of points of inflection for y=f(x) is….. .

The correct Answer is:2
Step by step video & image solution for The graph of y=f''(x) for a function f is shown. Number of points of inflection for y=f(x) is….. . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHS ENGLISHChapter:MONOTONICITY MAXIMA AND MINIMAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 29 Videos
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHS ENGLISHChapter:MONOTONICITY MAXIMA AND MINIMAExercise:Exercise (Single Integer Answer Type Questions)
Explore 11 Videos
- MATRICES Book:ARIHANT MATHS ENGLISHChapter:MATRICES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 49 Videos
- PAIR OF STRAIGHT LINES Book:ARIHANT MATHS ENGLISHChapter:PAIR OF STRAIGHT LINES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 2 Videos
Similar Questions
Knowledge Check

16-18 The graph of polynomial function f is shown above.
Q. What is the maximum number of points a circle whose center is at the origin can intersect the graph of y=f(x)?A2B3C4D6
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
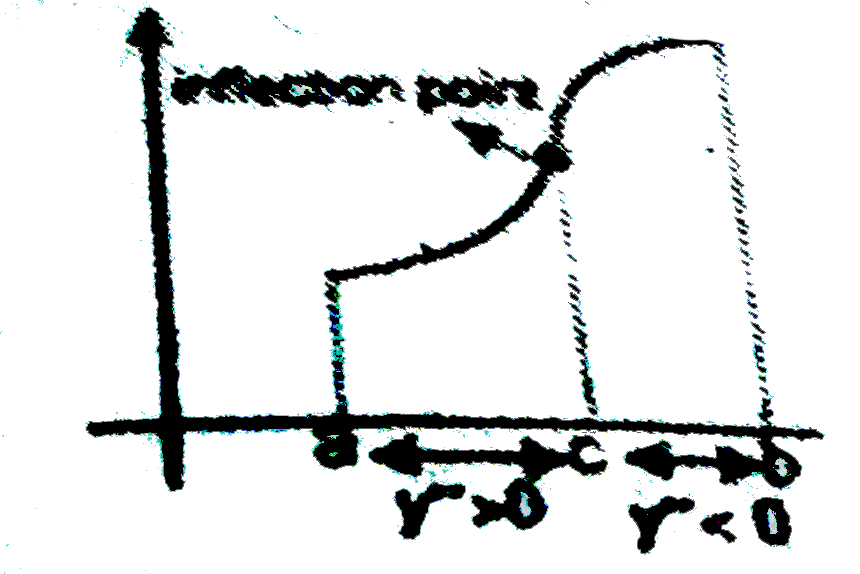
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionLet f(x)be real valued continous funcion on R defined as f(x) =x2e−|x|
Number of points of inflection for y=f(x) is (a) 1 (b) 2 (c) 3 (d) 4
View SolutionThe graph of y =g(x) =f(X) is as shown in the following figure analyse this graph and answer the following question

Number of points of inflectionn the graph of y = f(x) for a<x<b has
View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
View SolutionLet a differentiable function f:R→R be such that for all x and y in R
2|f(x)−f(y)|≤|x−y| and f′(x)≥12. So then the number of points of intersection of the graph y=f(x) with
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionIf A and B are the points of intersection of y=f(x) and y=f−1(x), then
View Solution



