In a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.
2
3
4
6
The correct Answer is:B
By triangle law, AB=AD−BD,AC=AD−CD
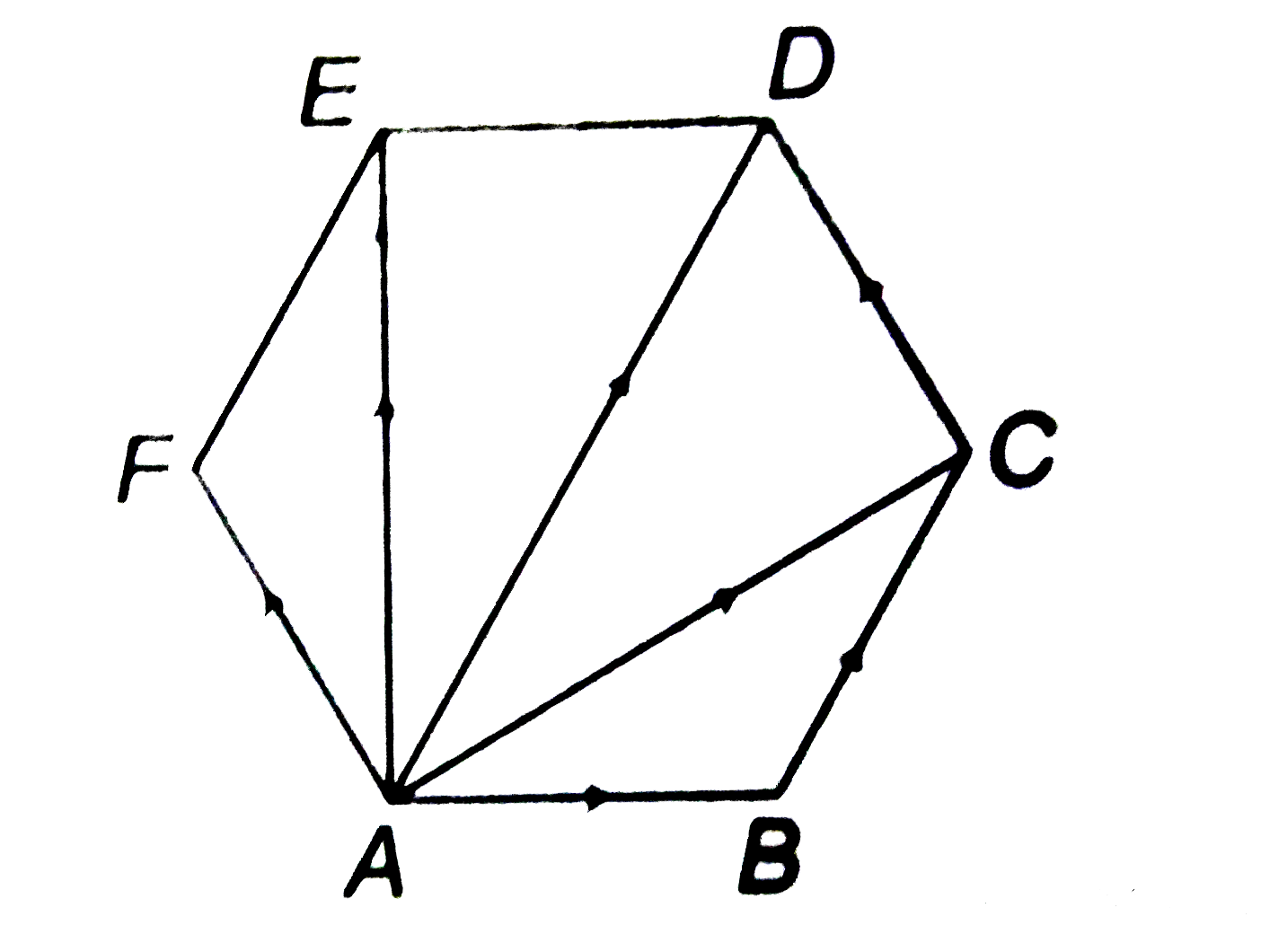
Therefore, AB+AC+AD+AE+AF
=3AD+(AE−BD)+(AF−CD)=3AD
hence, λ=3 (∵AE=BD,AF=CD)
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions
1 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
In a regular hexagon ABCDEF, −−→AE
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View SolutionIf ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB.
View SolutionABCDEF is a regular hexagon , with the sides AB, AC, AD, AE and AF representing vectors 1 unit , 2 units , 3 units , 4 units and 5 units respetively . Find their resultant ?
View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
View SolutionIf ABCDEF is a regular hexagon, prove that −−→AC+−−→AD+−−→EA+−−→FA=3−−→AB
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionAB is a side of a regular hexagon ABCDEF and is of length a with A as the origin and AB and AE as the x-axis andy-axis respectively. Find the equation of lines AC,AF and BE
View SolutionAB is a side of a regular hexagon ABCDEF and is of length a with A as the origin and AB and AE as the x-axis andy-axis respectively. Find the equation of lines AC,AF and BE
View SolutionIn a regular hexagon ABCDEF, AB||ED|| x-axis. What are the slopes of its sides?
View Solution
