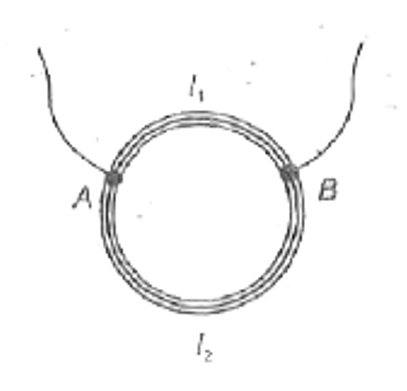
A ring is made of a wire having a resistance R0=12Ω. Find the point A and B as shown in the figure, at which a current carrying conductor should be connected so that the resistacne R of the sub circuit between these points is equal to 83Ω.
l1l2=38
l1l2=12
l1l2=58
l1l2=13
The correct Answer is:B
Since R∝l.
According to problem R1+R2=12Ω and R1×R2R1+R2=83Ω
On solving this we get R1=4Ω and R2=8Ω therefore the ratio l1l2=12
Similar Questions
In the circuit shown here, what is the value of the unknown resistor R so that the total resistance of the circuit between points P and Q is also equal to R

View Solution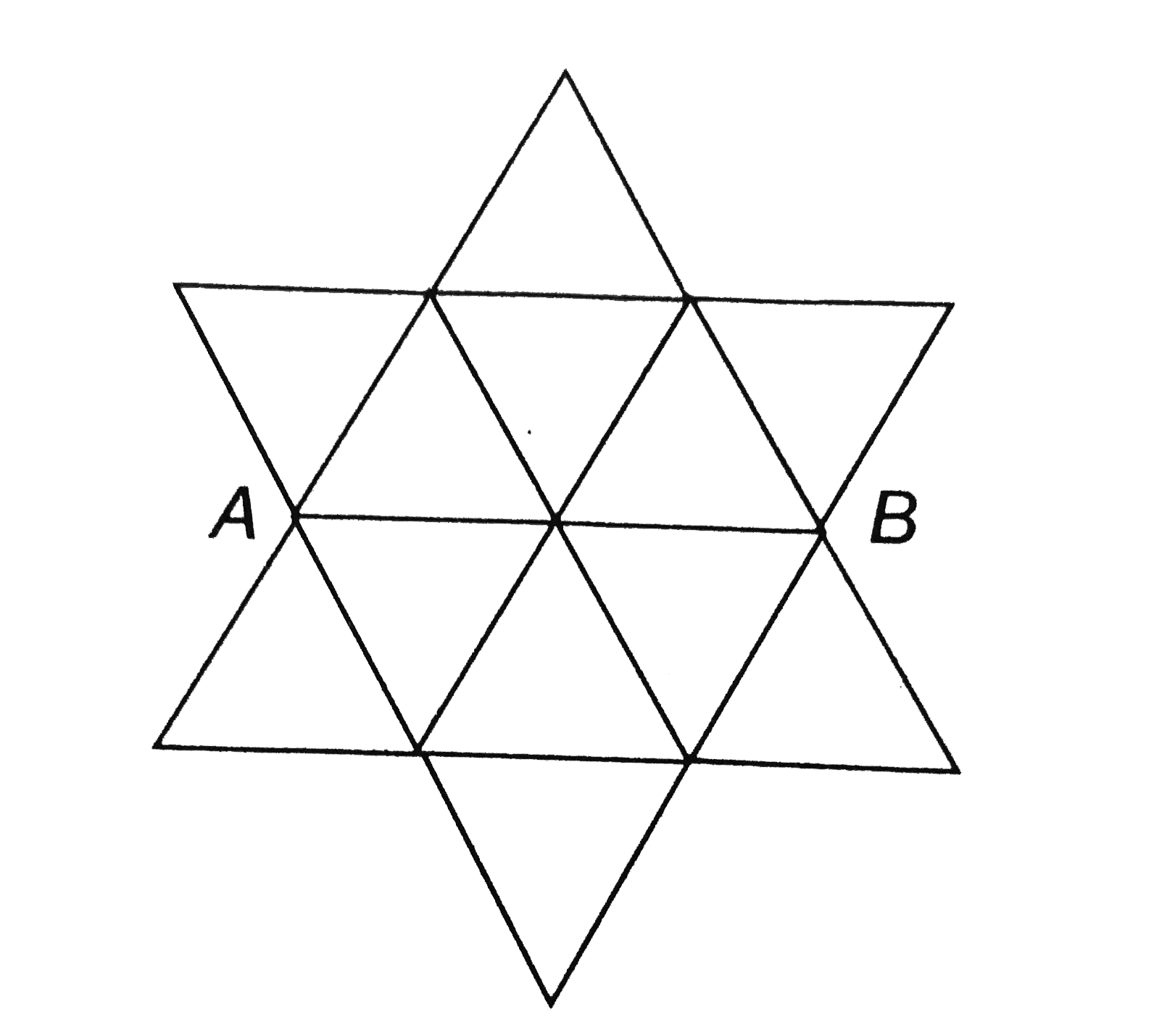
If the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is

View SolutionThe power dissipated in the resistance R, in the circuit as shown in the figure, is maximum if R is equal to
View SolutionThe equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionThe equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
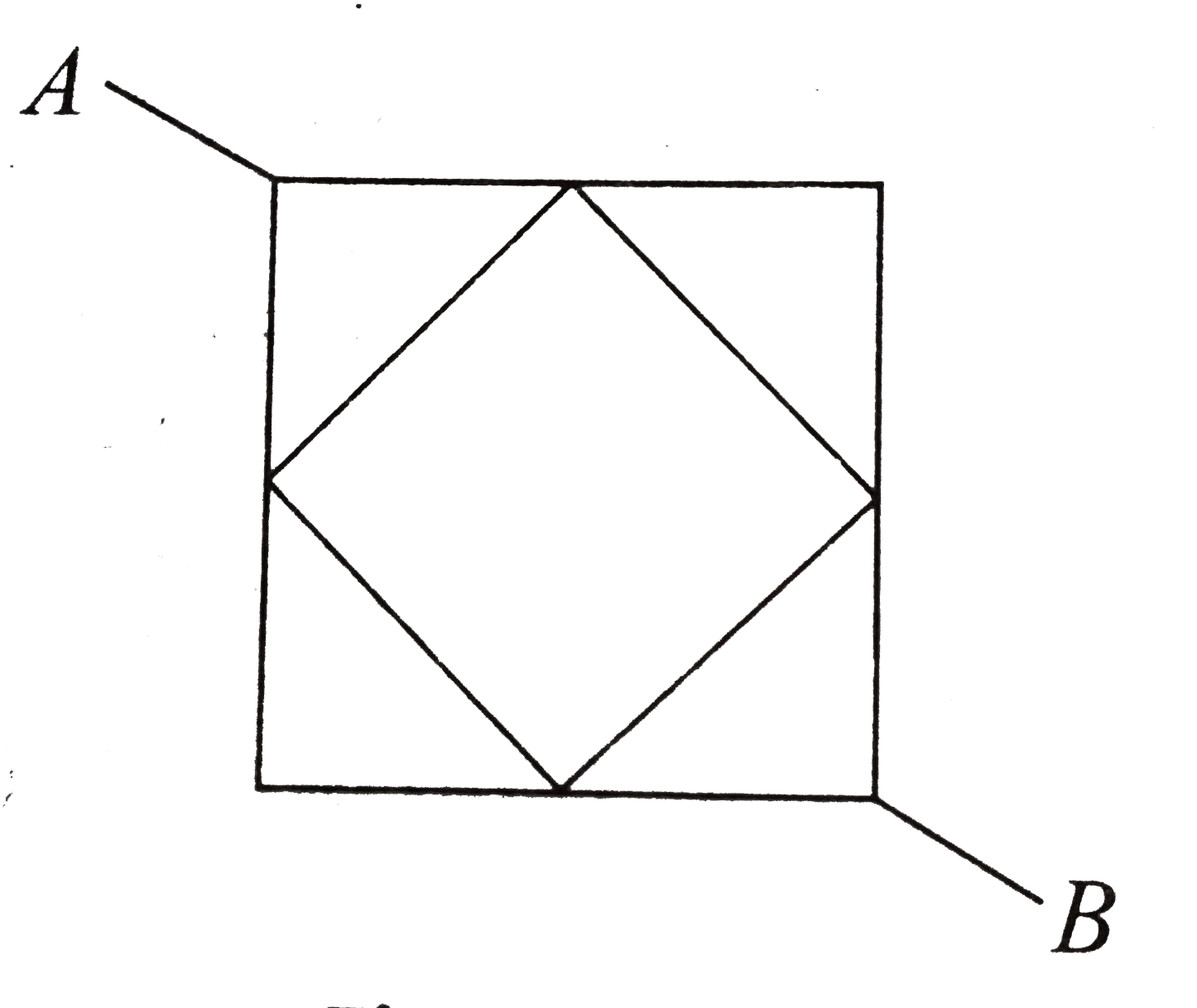
View SolutionA wire has linear resistance ρ (inΩm−1). Find the resistance R between points A and B if the side of the big square is d.
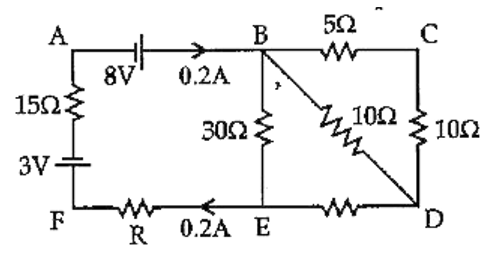
View SolutionCalculate the value of resistance R in the circuit shown in the figure so that the current in the circuits is 0.2A. What would be the potential difference between the points B and E ?
View SolutionFind the equivalent resistances between the points a and c of the network shown in figure. Each resistance is equal to r.
View SolutionIn the circuit shown, the value of each resistance is r , then equivalent resistance of circuit between points A and B will be

View Solution
