Answer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
Gauss. law : According to this law, the total flux linked with a closed surface called Gaussian surface, (the surface need not be a real physical surface, it can also be an hypothetical one) is (1ε0) times the charge enclosed by the closed surface i.e.,
ϕ=∮s→E.−→dA=1ε0(Qenc .
Similar Questions
Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionAnswer the following:
(a) State Gauss' law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
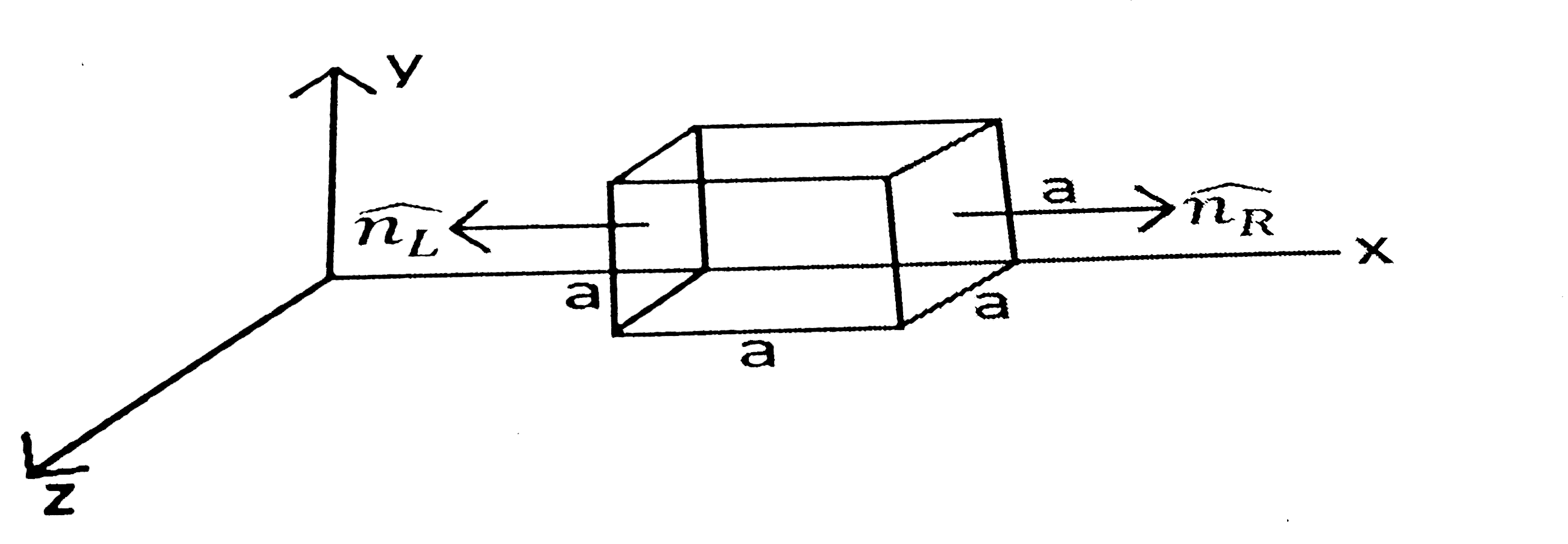
View SolutionAnswer the following:
(i) Use Gauss' law to find the electric field due to a uniformly charged infinite plane sheet. What is the direction of field for positive and negative charge densities?
(ii) Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitance in the ratio 1:2 so that the energy stored in the two cases becomes the same.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View Solution(a) Use Gauss's law to derive the expression for the electric filed (→E) due to straight uniformaly charges infinite line of charges density λC/m.
(b) Draw a graph to show the variation of E with perpendicular from the line of charge.
(c) Find the work done in brining a charge q from prependicular distance r1 to r2(r2>r1).
View Solution
