Question

Fig. show a conical pendulum. If the length of the pendulum is $l$, mass of die bob is m and $\theta$ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
$L=\sqrt{\frac{m^{2}g{l}^3{\sin }^4\theta }{\cos \theta }}$

Explanation

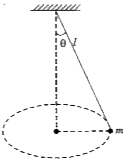
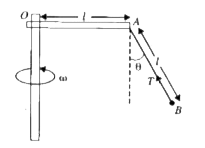
The forces acting on the bob are its weight mg acting vertically downwards and the tension acting along BA. The tension is resolved into two components `T cos theta` balances the weight of the bob.
`T cos theta =mg`……(i)
`T sin theta` provides the centripetal force. Total radius of the circular path is `l + l sin theta`. So centripetal force acting is `momega^(2)(l + l sin theta) = mlomega^(2) (1 + sin theta)`
`T sin theta = mlomega^(2)(1 + sin theta)`......(ii)
From eqns (i) and (ii)
`(T sin theta)/(T cos theta) = (ml omega^(2) (1 + sin theta))/(mg)`
`omega^(2) = (g tan theta)/(l(1+ sin theta))`
`omega = sqrt((g tan theta)/(1 (l + sin theta)))`