ABC is an acute-angled triangle incribed in a circle of radius 5 cm and centre O . The sine of angle A is equal to 35. Calculate without using tables :
(i) the length of BC
(ii) sin OBC
(iii) sin BOC
(iv) cos BOC
The correct Answer is:sin2A
To solve the problem step by step, we will calculate the required values based on the given information about triangle ABC inscribed in a circle of radius 5 cm with the sine of angle A being 35.
Step 1: Calculate the Length of BC
1. Given: Radius R=5 cm and sinA=35.
2. Using the formula for the length of side BC in a triangle inscribed in a circle:
BC=2RsinA
Substituting the values:
BC=2×5×35=6 cm
Step 2: Calculate sinOBC
1. Using the relationship between angles in triangle OBC:
∠BOC=2A
Since ∠OBC=∠OCB, we can denote ∠OBC=x.
Thus, we have:
∠BOC+2x=180∘⟹2A+2x=180∘⟹x=90∘−A
2. Using the sine of the angle:
sinOBC=sin(90∘−A)=cosA
3. Finding cosA using the Pythagorean identity:
sin2A+cos2A=1⟹(35)2+cos2A=1⟹925+cos2A=1
cos2A=1−925=1625⟹cosA=45
4. Thus,
sinOBC=45
Step 3: Calculate sinBOC
1. Using the double angle formula:
sinBOC=sin(2A)=2sinAcosA
2. Substituting the known values:
sinBOC=2×35×45=2425
Step 4: Calculate cosBOC
1. Using the Pythagorean identity:
cos2BOC+sin2BOC=1⟹cos2BOC+(2425)2=1
cos2BOC+576625=1⟹cos2BOC=1−576625=49625
cosBOC=725
Summary of Results
1. Length of BC=6 cm
2. sinOBC=45
3. sinBOC=2425
4. cosBOC=725
1. Given: Radius R=5 cm and sinA=35.
2. Using the formula for the length of side BC in a triangle inscribed in a circle:
BC=2RsinA
Substituting the values:
BC=2×5×35=6 cm
1. Using the relationship between angles in triangle OBC:
∠BOC=2A
Since ∠OBC=∠OCB, we can denote ∠OBC=x.
Thus, we have:
∠BOC+2x=180∘⟹2A+2x=180∘⟹x=90∘−A
2. Using the sine of the angle:
sinOBC=sin(90∘−A)=cosA
3. Finding cosA using the Pythagorean identity:
sin2A+cos2A=1⟹(35)2+cos2A=1⟹925+cos2A=1
cos2A=1−925=1625⟹cosA=45
4. Thus,
sinOBC=45
1. Using the double angle formula:
sinBOC=sin(2A)=2sinAcosA
2. Substituting the known values:
sinBOC=2×35×45=2425
1. Using the Pythagorean identity:
cos2BOC+sin2BOC=1⟹cos2BOC+(2425)2=1
cos2BOC+576625=1⟹cos2BOC=1−576625=49625
cosBOC=725
1. Length of BC=6 cm
2. sinOBC=45
3. sinBOC=2425
4. cosBOC=725
Topper's Solved these Questions
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - EXERCISE 5 (D)
60 Videos
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - CHEPTER TEST
23 Videos
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - EXERCISE 5 (B)
35 Videos
- COMPLEX NUMBERSBOOK - ICSECHAPTER - COMPLEX NUMBERSEXERCISE - Chapter Test
25 Videos
- CONIC SECTIONS BOOK - ICSECHAPTER - CONIC SECTIONS EXERCISE - Multiple Choice Questions
33 Videos
Similar Questions
In the given on equilateral triangle ABC is inscribed in a ciecle with centre O. Find:
∠OBC and ∠BOC
View SolutionFind the angle subtended at the centre of a circle of radius 5 cm by an arc of length (5π/3)cm .
View SolutionIn a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110o at the centre of the circle. Find (i) the length of the arc AB , (ii) the area of the sector OAB .
View SolutionIf A is an obtuse angle whose sine is 513andB is an acute angle whose tangent is 34, without using tables find the values of
(a) sin2B,
(b)tan(A−B).
View SolutionDraw a circle of radius 3.5 cm with centre O. Draw two tangents to the circle so that the angle. Between tangent is 60∘.
View SolutionIn a circle of radius 21 cm, an arc subtends an angle of 60o at the centre. Find: (i) length of the arc
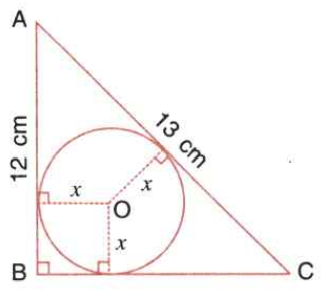
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionUsing ruler and compasses only, construct
construct a circle of radius 2.5 cm which touches the arms of the angle BAC ofΔABC.
View SolutionThe sides of a triangle containing the right angle are 5x cm and (3x−1) cm. If the area of the triangle is 60 cm2, calculate the lengths of the sides of the triangle.
View SolutionIn a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110o at the centre of the circle. Find (i) the circumference of the circle, (ii) the area of the circle
View Solution
