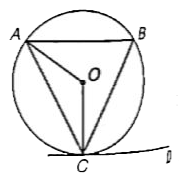
In the given diagram O is the centre of the circle and CD is a tangent. ∠CAB and ∠ACD are supplementary to each other ∠QAC=30∘. Find the value of ∠OCB.
30∘
20∘
60∘
none of these
The correct Answer is:A
To solve the problem, we need to find the value of angle OCB given the information provided. Here’s a step-by-step solution:
Step 1: Identify the angles and their relationships
We know that:
- Angle CAB and angle ACD are supplementary, meaning their sum is 180 degrees.
- Angle QAC is given as 30 degrees.
We know that:
- Angle CAB and angle ACD are supplementary, meaning their sum is 180 degrees.
- Angle QAC is given as 30 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
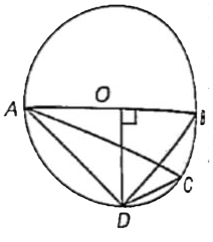 A30∘B60∘C45∘D25∘
A30∘B60∘C45∘D25∘In the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
 AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+ACIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
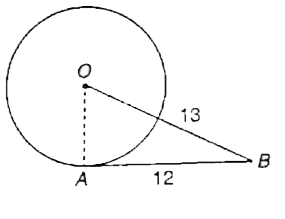 A6.5 cmB6 cmC5 cmDnone of these
A6.5 cmB6 cmC5 cmDnone of these
If figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
View SolutionIn the given figure O is the centre of the circle and AB||CD. If ∠ADC=25∘, then find ∠AEB∘-

View SolutionIn the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionIn the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD

View Solution