In a bangle shop, the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles with him. If he wanted to increase the size of square by one unit each side of the square he found that 25 bangles fall short of in completing the square. The actual number of bangles which he had with him in the shop was :
1690
999
538
can't be determined
The correct Answer is:B
Step by step video, text & image solution for In a bangle shop, the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles with him. If he wanted to increase the size of square by one unit each side of the square he found that 25 bangles fall short of in completing the square. The actual number of bangles which he had with him in the shop was : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A teacher on attempting to arrange the students for mass drill in the form of a solid square found that 24 students were left. when he increased the size of the square by one student,he found that he was short of 25 students find the number of students.
View SolutionA teacher on attempting to arrange the students for mass drill in the form of a solid square found that 24 students were left. When he increased the size of the square by one student, he found that he was short of 25 students. Find the number of students.
View Solution
Knowledge Check
In a bangle shop, the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles with him. If he wanted to increase the size of square by one unit each side of the square he found that 25 bangles fall short of in completing the square. The actual number of bangles which he had with him in the shop was :
A1690B999C538Dcan't be determinedOne day my assistant Rajesh went to a stationary shop to purchase marker pens.He purchased the pens for ₹52 and he gave a ₹100 note to the shopkeeper The shopkeeper offered Rajesh to take back ₹48in the denominations of only ₹1,₹2 and ₹5 .so Rajesh received total 26 coins from the shopkeeper Minimum number of ₹1 coins which Rajesh has with him if he has atleasst one coin of each denomination offered by the shopkeeper:
A4B5C7D10King Dashratha of Ayodhya had a rectangular plot of area 9792m2. He divided it into 4 square shaped plots by fencing parallel fences to the breadth of the rectangular plot. All the four sons got each square shaped plot. However , same area of plot was still left which could not be formed as a square shaped. So, four more square shaped plots were formed by fencing parallel to the longer side of the original plot. The king gave one smaller square shaped plot to each of his wives and one of the smaller square shaped plot retained with himself and then nothing left to divide .
What is the ratio of the area of larger square shaped plot to the area of the smaller square shaped plot ?A17:1B25:9C16:1Dcan't be determined
A General of an Army wants to create a formation of square from 36562 army men. After arrangement, he found some army men remained unused. Then the number of such army men remained unused was
View SolutionA General wishes to draw up his 7500 soldiers in the form of a square. After arranging, he found out that some of them are left out. How many soldiers were left out?
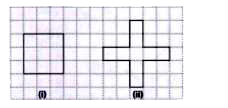
View SolutionAvneet buys 9 square paving slabs, each with a side of 12m. He lays them in the form of a square.
Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [see fig. (ii)]
View SolutionA General of an Army wants to create a formation of square from 36562 army men. After arrangement, he found some army men remained unused. Then the number of such army men remained unused was
View SolutionKing Dashratha of Ayodhya had a rectangular plot of area 9792m2. He divided it into 4 square shaped plots by fencing parallel fences to the breadth of the rectangular plot. All the four sons got each square shaped plot. However , same area of plot was still left which could not be formed as a square shaped. So, four more square shaped plots were formed by fencing parallel to the longer side of the original plot. The king gave one smaller square shaped plot to each of his wives and one of the smaller square shaped plot retained with himself and then nothing left to divide .
What are dimensions of the original plot ?
View Solution
