A body moving with a speed of 54kmph is brought to rest in a distances. If the coefficient of friction between the body and the surface is 0.3. Calculate the distance travelled by the body ?
To solve the problem step by step, we will follow the outlined approach in the video transcript.
Step 1: Convert Speed from km/h to m/s
The speed of the body is given as 54 km/h. We need to convert this into meters per second (m/s).
Speed in m/s=Speed in km/h×518
Calculating:
Speed=54×518=15 m/s
Step 2: Identify the Coefficient of Friction
The coefficient of friction (μ) is given as 0.3.
Step 3: Calculate the Acceleration Due to Friction
The force of friction (F) can be expressed as:
F=μR
Where R is the normal reaction force, which for a horizontal surface is equal to the weight of the body (mg). Thus, we have:
R=mg
Substituting this into the force equation gives:
F=μmg
Using Newton's second law, F=ma, we can equate the two expressions:
ma=μmg
We can cancel m from both sides (assuming m≠0):
a=μg
Assuming g≈10 m/s2:
a=0.3×10=3 m/s2
Since this is a deceleration (the body is coming to rest), we take it as negative:
a=−3 m/s2
Step 4: Use the Equation of Motion to Find Distance
We will use the third equation of motion:
v2=u2+2as
Where:
- v=0 (final velocity, since the body comes to rest)
- u=15 m/s (initial velocity)
- a=−3 m/s2 (acceleration)
Substituting the values into the equation:
0=(15)2+2(−3)s
This simplifies to:
0=225−6s
Rearranging gives:
6s=225
Dividing both sides by 6:
s=2256=37.5 m
Final Answer
The distance traveled by the body before coming to rest is 37.5 meters.
---
The speed of the body is given as 54 km/h. We need to convert this into meters per second (m/s).
The coefficient of friction (μ) is given as 0.3.
The force of friction (F) can be expressed as:
We will use the third equation of motion:
- v=0 (final velocity, since the body comes to rest)
- u=15 m/s (initial velocity)
- a=−3 m/s2 (acceleration)
The distance traveled by the body before coming to rest is 37.5 meters.
Topper's Solved these Questions
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Additional solved examples
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer
9 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
Similar Questions
If angle of repose is ϕ, the coefficient of static friction between body and the plane is
View SolutionA body is moving is down an inclined plane of slope 37∘ the coefficient of friction between the body and the plane varies as μ=0.3x, where x is the distance traveled down the plane by the body. The body will have maximum speed. (sin37∘=35) . a) at x = 1.16 m b) at x = 2m c) at bottom most point of the plane d) at x = 2.5 m
View SolutionA body starts from rest on a long inclined plane of slope 45∘ . The coefficient of friction between the body and the plane varies as μ=0.3x , where x is the distance travelled down the plane. The body will have maximum speed (for g=10m/s2 ) when x =
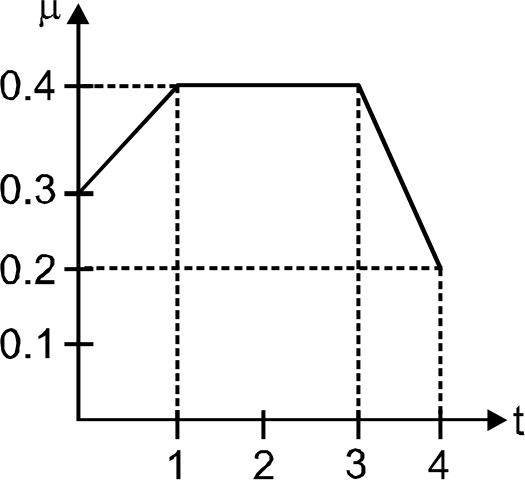
View SolutionA small body is projected with a velocity of 20.5ms−1 along rough horizontal surface. The coefficient of friction (μ) between the body and surface changes with time t (in s) as the the body moves along the surface. Find the velocity at the end of 4s in m/s
View SolutionA body of mass 5kg is under the action of 50N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 3 s is
View SolutionA body is moving down along inclined plane of angle of inclination q. The coefficient of friction between the body and the plane varies as mu = 0.5x, where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by
View SolutionA body moving on a surface is brought to rest suddenly. What happens to the friction between the two ?
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
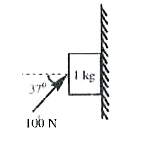
View SolutionA body of mass 10kg is under the action of 138N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 10s in metre is
View SolutionA body is in contact with the vertical front part of the truck. The coefficient of friction between the body and the truck is μ. The minimum acceleration with which the truck should travel so that the body does not fall down is
View Solution
