vertex and focus of a parabola are (-1,1) and (2,3) respectively. find the equation of the directrix.

A

$3 x + 2 y + 14 = 0$

B

$3 x + 2 y - 25 = 0$

C

$2 x - 3 y + 10 = 0$

D

$x - y + 5 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

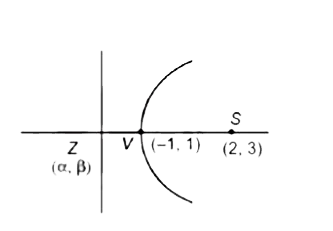
As we know that, vertex is the mid-point of the perpendicular drop from the focus of the directrix.
$\frac{α + 2}{2} = - 1 \Rightarrow α + 2 = - 2 \Rightarrow α = - 4$
$\frac{β + 3}{2} = 1 \Rightarrow β = 2 - 3 = - 1$
Slope of axis of the parabola $= \frac{3 - β}{2 - α} = \frac{3 + 1}{2 + 4} = \frac{2}{3}$
Slope of the directrix $= - \frac{3}{2}$
Equation of directrix is
$y + 1 = - \frac{3}{2} (x + 4)$
$2 y + 2 = - 3 x - 12$
$3 x + 2 y + 14 = 0$

Updated on:21/07/2023

|

Class 11 MATHS QUIZ

Similar Questions

Knowledge Check

If the focus and the vertex of a parabola are (2,3) and (-1,1) respectively, then the directrix is :
A $3 x + 2 y + 14 = 0$
B $3 x + 2 y - 25 = 0$
C $2 x - 3 y + 10 = 0$
D $2 x - 3 y + 14 = 0$

Recommended Questions

Home
Ask Doubt
Profile