A par sec is a convenient unit of length on the astronomical scale. It is the distance o an object that will show a parallax of 1 s of arc from opposite ends of a base line equal to the distance from the earth to the sun. How much is a sec in terms of metre?
To solve the problem of converting a par sec (parsec) into meters, we will follow these steps:
1. Understanding the Definition of Parsec:
- A parsec is defined as the distance at which an object shows a parallax of 1 arcsecond when viewed from two points separated by a distance equal to 1 astronomical unit (AU), which is the average distance from the Earth to the Sun.
2. Identifying the Values:
- 1 AU = 1.5×1011 meters.
- The angle of parallax, θ, is given as 1 arcsecond.
3. Convert Arcseconds to Radians:
- We need to convert the angle from arcseconds to radians because the formula for parallax uses radians.
- There are 3600 arcseconds in a degree and 180 degrees in a radian.
- Therefore, to convert 1 arcsecond to radians:
θ=1 arcsecond=13600 degrees=13600×π180 radians
- Simplifying this gives:
θ=π648000 radians
4. Using the Parallax Formula:
- The relationship between arc length (which is the baseline, or 1 AU), radius (which is the distance in parsecs), and angle in radians is given by:
θ=arc lengthradius
- Rearranging this gives:
radius=arc lengthθ
5. Substituting the Values:
- Substituting the values we have:
radius=1.5×1011 metersπ648000
6. Calculating the Radius (Parsec):
- Now, we can calculate the radius:
radius=1.5×1011×648000π
- Using π≈3.14159, we can compute:
radius≈1.5×1011×6480003.14159≈3.1×1016 meters
7. Final Result:
- Therefore, 1 parsec is approximately 3.1×1016 meters.
Final Answer:
1 parsec = 3.1×1016 meters.
---
- A parsec is defined as the distance at which an object shows a parallax of 1 arcsecond when viewed from two points separated by a distance equal to 1 astronomical unit (AU), which is the average distance from the Earth to the Sun.
- 1 AU = 1.5×1011 meters.
- The angle of parallax, θ, is given as 1 arcsecond.
- We need to convert the angle from arcseconds to radians because the formula for parallax uses radians.
- There are 3600 arcseconds in a degree and 180 degrees in a radian.
- Therefore, to convert 1 arcsecond to radians:
θ=1 arcsecond=13600 degrees=13600×π180 radians
- Simplifying this gives:
θ=π648000 radians
- The relationship between arc length (which is the baseline, or 1 AU), radius (which is the distance in parsecs), and angle in radians is given by:
θ=arc lengthradius
- Rearranging this gives:
radius=arc lengthθ
- Substituting the values we have:
radius=1.5×1011 metersπ648000
- Now, we can calculate the radius:
radius=1.5×1011×648000π
- Using π≈3.14159, we can compute:
radius≈1.5×1011×6480003.14159≈3.1×1016 meters
- Therefore, 1 parsec is approximately 3.1×1016 meters.
1 parsec = 3.1×1016 meters.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS)5videos
UNITS
- BOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)3videos
UNITS
- BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)14videos
THERMAL RADIATION
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS79videos
VECTORS SCALARS ELEMENTARY CALCULUS
Similar Questions
A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the sun and the earth in terms of the new unit, if light takes 8 min and 20 sec. to cover the distance ?
View SolutionSTATEMENT -1 : In summers, the distance of earth from the Sun is less than one astronmical unit, while in winters, it is more than one astronomical unit.
and
STATEMENT -2 : One astronomical unit is the average distance of earth from the Sun when the earth moves in an ellipitical orbit.View Solution
Knowledge Check
- Question 1 - Select One
A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the sun and the earth in terms of the new unit, if light takes 8 min and 20 sec. to cover the distance ?
A300B400C500D600
Figure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
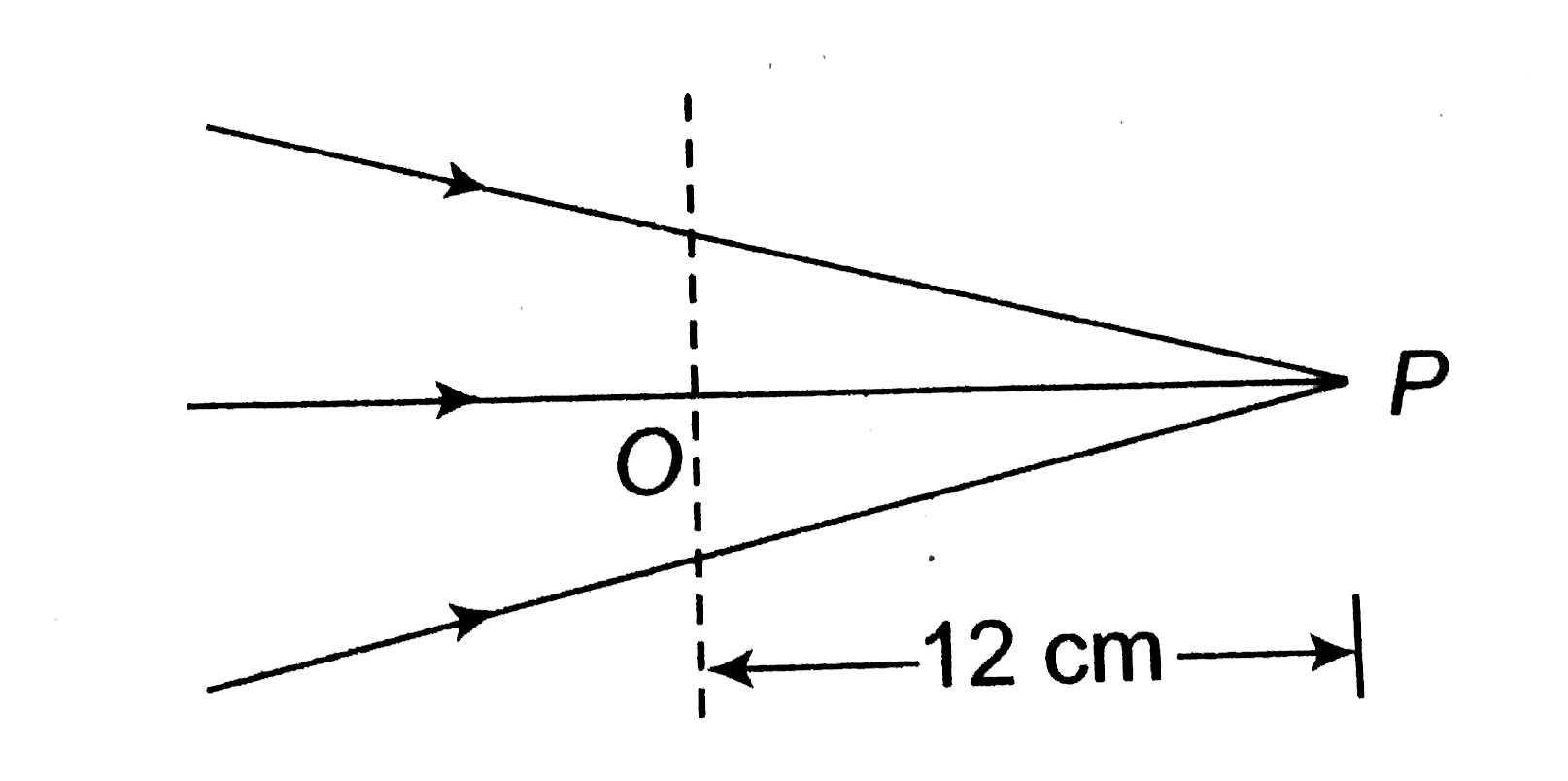 View Solution
View SolutionA particle is dropped from the top of a tower. Its covered distance in last 1 sec is equal to distance covered by particle in 1st3s. Find height of tower.
View SolutionA lamp post of length 10 meter placed at the end A of a ladder AB of length 13 meters, which is leaning against a vertical wall as shown in figure and its base slides away from the wall. At the instant base B is 12 m from the vertical wall, the base B is moving at the rate of 5 m/sec. A man (M) of height 1.5 meter standing at a distance of 15 m from the vertical wall.

The rate at which the length of shadow of man increases, when the base B is 12 m from vertical wall, isView SolutionA lamp post of length 10 meter placed at the end A of a ladder AB of length 13 meters, which is leaning against a vertical wall as shown in figure and its base slides away from the wall. At the instant base B is 12 m from the vertical wall, the base B is moving at the rate of 5 m/sec. A man (M) of height 1.5 meter standing at a distance of 15 m from the vertical wall.

Rate at which θ decreases, when the base B is 12 m from the vertical wall, isView SolutionFigure shows a fish bowl of radius 10 cm in which along a diametrical line a fish F is moving at speed 2 mm/sec. Find the speed of fish as observed by an observer from outside along same line when fish is at a distance 5 cm from the centre of bowl to right of it as shown in figure

3.84 mm/sView SolutionTwo particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionA smooth disc of mass M and radius L√3 is placed at rest horizontally on a smooth horizontal surface. A massless pin is fixed at point P at a distance L/2 from centre O of the disc as shown in the figure. Now a thin uniform rod of mass M and length L is placed horizontally on the surface of the disc parallel to the line OP such that its mid point and centre O of the disc just coincide as shown in figure. Now rod has given angular velocity ω0=24rad/sec in counter clockwise direction as shown. As a result, the end of the rod strikes the pin P and stricks to it rigidly. Calculate the angular velocity of disc just after collision.
 View Solution
View Solution
