A black and red dice are rolled. Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5 Solution in Malayalam
If the event that the "blacl die is resulted in 5" is given then the possible elementary cases under consideration are reduced to (5,1),(5,2),(5,3),(5,4),(5,5),(5,6). Out of these 6 cases only two cases are favourable to the event that sum of the number rolled is greater than 9.
therefore Required probability =2/6=1/3.
Topper's Solved these Questions
Similar Questions
Consider the following information regarding the purchase of pens and penciles by the three students Ravi, Twinkle and Lal from a shop.
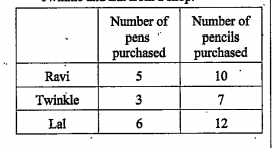 Represent the above data in the form of a 3×2 matrix. What does the entry in the 2nd row and in the first column represent?
Represent the above data in the form of a 3×2 matrix. What does the entry in the 2nd row and in the first column represent?
View SolutionLet A be the set of all 50 students of class X in a school. Let f:A→N
be function defined by f(x) = roll numbers of the student x. Show that
f is one-one but not onto
View SolutionA black and a red dice are rolled.(a) Find the conditional probability of obtaining a sum greater than 9. Given that the black die resulted in a 5.(b) Find the conditional probability of obtaining the sum 8? given that the red die resulted in a number less than 4.
View SolutionA black and a red die are rolled.
Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5 .
View SolutionA black and a red die are rolled.
Find the conditional probability of obtaining the sum 8, given that the red dieresulted in a number less than 4 .
View SolutionA black and a red die are rolled together. Find the conditional brobability of obtaining the sum 8, given that the red die resulted a number less than 4.
View SolutionA black and red dice are rolled.
a. Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
b. Find the conditional probability of obtainingthe sum 8, given that the red die resulted in a number less than 4.
View SolutionA black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
View SolutionA black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
View SolutionA black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
View SolutionA black and a red dice are rolled. (a) Find the conditional probability of obtaining a sum greater than 9. Given that the black die resulted in a 5. (b) Find the conditional probability of obtaining the sum 8? given that the red die resulted in a number less than 4.
View SolutionA black and a red dice are rolled. (a) Find the conditional probability of obtaining a sum greater than 9. Given that the black die resulted in a 5. (b) Find the conditional probability of obtaining the sum 8? given that the red die resulted in a number less than 4.
View SolutionA black and a red dice are rolled. (a) Find the conditional probability of obtaining a sum greater than 9. Given that the black die resulted in a 5. (b) Find the conditional probability of obtaining the sum 8? given that the red die resulted in a number less than 4.
View SolutionA black and red dice are rolled. Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5
View SolutionA black and red dice are rolled. Find the conditional probability of obtaining a sum 8, given that the red die resulted in a number less than 4
View SolutionTwo dice, one black and one white are rolled. The probability that sum of two no is 7 and no. of black greater than the no. of white is
View Solution
