∫(x2+1)xx4−1dx=
ln(√x2−1)+C
12ln(√x2−1+C
12ln(√x2−1)+C
ln(x2+1)2+C
The correct Answer is:A
∫xdx(x2−1)=ln(√x2−1)+C
Topper's Solved these Questions
Similar Questions
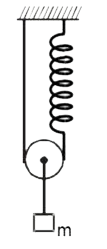
निकाय विराम अवस्था से छोड़ा जाता है। स्प्रिंग प्रारम्भ में अपनी लम्बाई है। यदि ब्लॉक का द्रव्यमान M = 10 Kg है , तथा स्प्रिंग नियतांक k = 100 N/m है , तब स्प्रिंग में अधिकतम विस्तार होगा
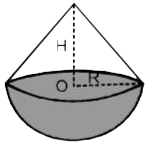
View Solutionएक समांग वस्तु में एक शंकु के वत्ताकार भाग R = m त्रिज्या के एक अर्द्धगोलाकार भाग से जुड़ा है। यदि सम्पूर्ण वस्तु का गुरुत्व केंद्र शंकु के वत्ताकार आधार के केंद्र O से सम्पाती है तो शंकु की ऊँचाई H ज्ञात करो।
View Solution∫x2+1x4+x2+1dx
View Solution∫x2−1x4−x2+1dx
View Solutionint(x^(4))/(1+x^(2))dx
View Solution∫x4+1x(x2+1)2dx
View Solution∫ x2x4−1 dx
View Solution(i) ∫(x2−1x2+1)dx , (ii) ∫(x6−1x2+1)dx
(iii) ∫(x41+x2)dx , (iv) ∫(x21+x2)dx
View Solution∫x2+1x4−x2+1dx= . . .
View Solution∫x2+1x4−x2+1dx=
View Solution∫x2−1x4+x2+1dx=
View Solutionमूल्यांकित कीजिये ∫1x(x4−1)dx=∫1x(x+1)(x−1)(x2+1)dx
View Solution∫x4x2+1dx
View Solution∫x2+1x4+x2+1dx=
View Solution∫x2+1x4+x2+1dx
View Solution∫(x2−1)dxx4+x2+1
View Solution
