A particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t3.
Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 secSolution in Telugu
The correct Answer is:(i) 20 cm/sec (ii) 8 cm/sec (iii) 12 cm/sec2
Step by step video & text solution for A particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t^3. Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 sec by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RATE OF CHANGEBOOK - AAKASH SERIESCHAPTER - RATE OF CHANGEEXERCISE - Advanced Analytical Solved Examples
3 Videos
- RATE OF CHANGEBOOK - AAKASH SERIESCHAPTER - RATE OF CHANGEEXERCISE - Exercise 6.1 (SHORT ANSWER QUESTIONS)-I
5 Videos
- RATE MEASUREMENTBOOK - AAKASH SERIESCHAPTER - RATE MEASUREMENTEXERCISE - PRACTICE SHEET (EXERCISE - 1) (LEVEL - 1) (STRAIGHT OBJECTIVE TYPE QUESTION)
43 Videos
- REAL FUNCTIONS BOOK - AAKASH SERIESCHAPTER - REAL FUNCTIONS EXERCISE - EXERCISE-1
34 Videos
Similar Questions
On the curve x3=12y, find the interval of value of x for which the abscissa changes at a faster rate than the ordinate?
View SolutionThe displacement s of a particle travelling in a straight line in t seconds is given by s=45t+11t2−t3. Find the time when the particle comes to rest.
View SolutionIf a particle moves alonga straight line by S=4t2−8t+3 and the time at which the particle comes of rest is 't' seconds then '2t' is
View SolutionFind the domains of the following functions
f(x)=x2+x+1
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
View Solutionएक कण एक सीधी रेखा में गतिमान है। सेकण्ड बाद रेखा में दिये गये बिन्दु से इसकी दूरी मीटर में s=t33−t22−6t+5 द्वारा प्रदत्त है। तब ज्ञात कीजिए-
(i) 5 सेकण्ड बाद कण का वेग क्या होगा? था
(ii) जब कण का वेग शून्य है तब इसका त्वरण क्या होगा?
View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
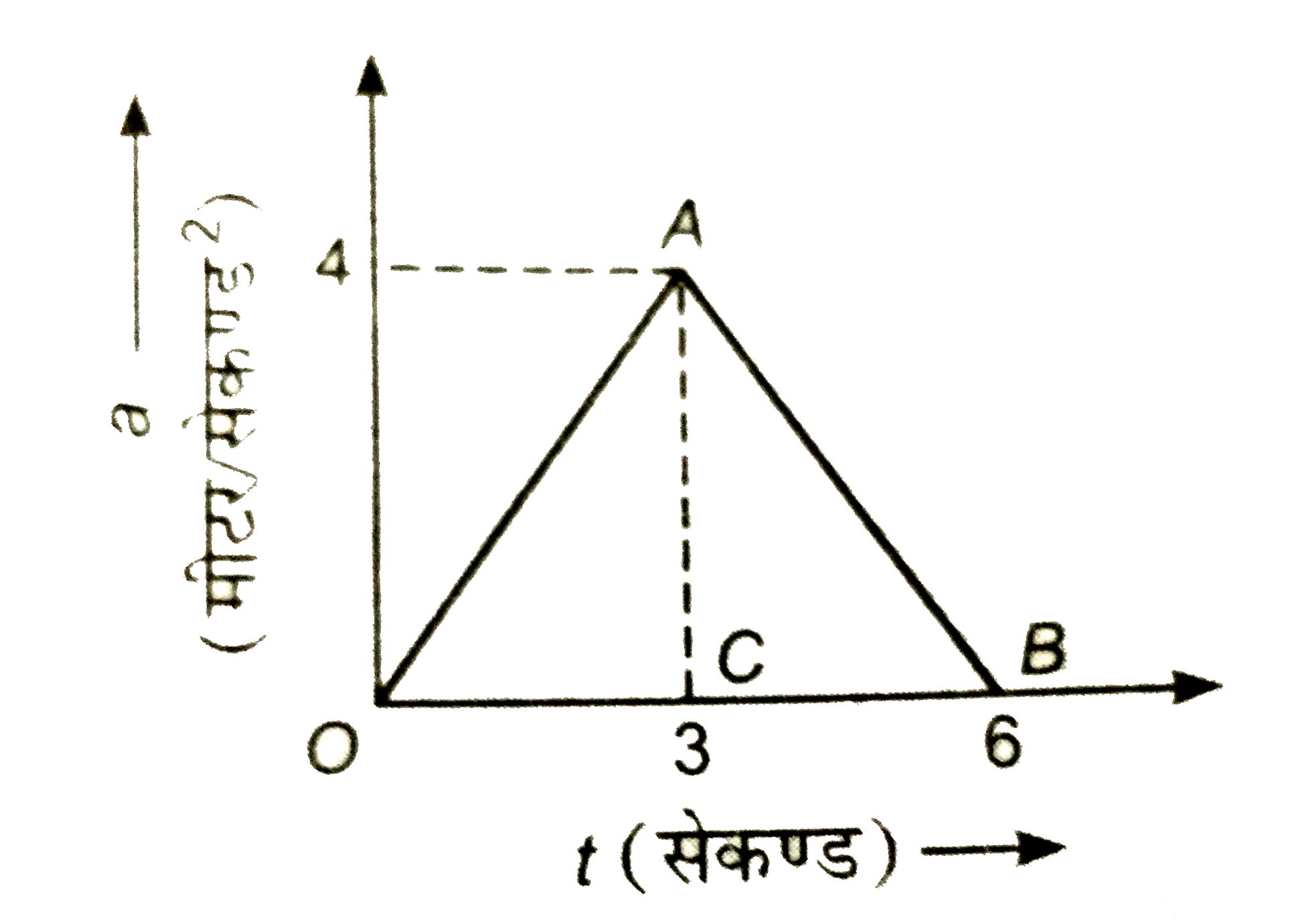
View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
View Solutionएक कण एक सरल रेखा में इस तरह से चलता हैं ताकि इसका स्थिति t सेकेण्ड के बाद s(t)=6t−t2 हैं | इसका प्रारंभिक वेग क्या हैं।
View SolutionA particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t3.
Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 sec
View SolutionA particle is moving in a straight line and its distance x cm from a fixed point on the line at any time t seconds is given by ,
x=112t4−23t3+32t2+t+15.
At what time is the velocity minimum ? Also find the minimum velocity.
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
View SolutionA particle moves in a straight line such that its distance in 't' seconds from a fixed point is (6t−t2) cm. find its velocity at the end of t=2 sec.
View SolutionA particle is moving in a straight line is at a distance S from a point O on the line in time t, where S=t3−6t2+8t+5.Find the velocity when the acceleration is 12cm/sec2.
View Solution
