माना M एक 2×2 आव्यूह इस प्रकार है की M[1−1]=[−12] तथाM2[1−1]=[10] है यदि x1और x2 (जहाँ x1>x2)के दो मान हो जिसके लिए det (M−xI)=0 है जहाँ I एक 2 कोटि का तत्समक आव्यूह है , तो (5x1+2x2)का मान ज्ञात कीजिये।
The correct Answer is:8
Step by step video, text & image solution for माना M एक 2xx2 आव्यूह इस प्रकार है की M [(1),(-1)]=[(-1),(2)] तथाM^(2)[(1),(-1)] =[(1),(0)] है यदि x_(1)और x_(2) (जहाँ x_(1)gt x_(2))के दो मान हो जिसके लिए det (M-xI)=0 है जहाँ I एक 2 कोटि का तत्समक आव्यूह है , तो (5x_(1)+2x_(2))का मान ज्ञात कीजिये। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DETERMINANT & MATRICSBOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -3 SECTION -A (JEE-ADVANCED Previous Year.s Questions) (Determinants)
6 Videos
- DETERMINANT & MATRICSBOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -3 SECTION -A (JEE-ADVANCED Previous Year.s Questions) (Matrics)
25 Videos
- DETERMINANT & MATRICSBOOK - BANSAL HINDICHAPTER - DETERMINANT & MATRICSEXERCISE - EXERCISE -2 SECTION -A [DETERMINANT]
30 Videos
- CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)BOOK - BANSAL HINDICHAPTER - CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)EXERCISE - EXERCISE - 5
18 Videos
- INDEFENITE & DEFINITE INTEGRATION BOOK - BANSAL HINDICHAPTER - INDEFENITE & DEFINITE INTEGRATION EXERCISE - EXERCISE -5 ( Rank Booster)
23 Videos
Similar Questions
माना तीन बिन्दु
P=(−sin(β−α),−cosβ),Q=(cos(β−α),sinβ) तथा R=(cos(β−α+θ),sin(β−θ)) है, जहाँ 0<α,β,θ<π4
View Solutionस्तम्भ I में कथनों/व्यजनों को स्तम्भ-II में कथनों/व्यंजकों से मिलाईये तथा अपने OMR में दिए 4×4 आव्यूह में उचित गोले को कला करके निर्देशित कीजिये |
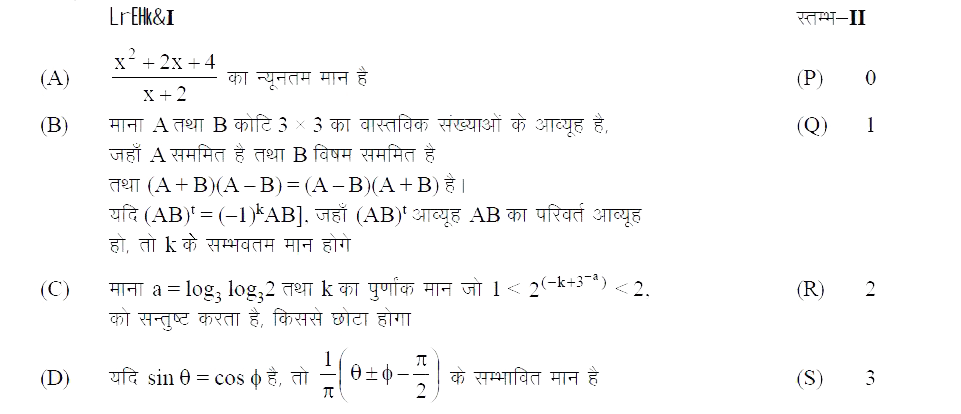
View Solutionसिद्ध कीजिये की सारणिक ∣∣ ∣ ∣∣−75+3i23−4i5−3i84+5i23+4i4−5i9∣∣ ∣ ∣∣ का मान वास्तविक है
View Solutionबिन्दु P(h, k) से परवलय x2=8y पर तीन अभिलम्ब डाले गये है तथा m1,m2 तथा m3 इन तीनों की प्रवणताऐं है। इन तीनों अभिलम्बों की प्रवणताओं का बीजगणितीय योग ज्ञात कीजिए।
View Solutionनिम्नलिखित समाकल का मान ज्ञात कीजिए-
∫sin−1√xa+xdx.
View SolutionSolve following L.P.P by graphical method: Z=5x1+6x2,x1+x2≥50,x1+2x2≤40,3x1+4x2≤100,x1,x2≥0
View Solutionनिम्न रैखिक युगपत समीकरण को हल कीजिए -
x1+x2+x3=9
2x1+5x2+7x3=52
2x1+x2−x3=0
View Solutionमान X एक याद्द्च्छिक चर है जो मान x1,x2,x3,x4 इस प्रकार ग्रहण करता है कि 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4) चर X का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionλ के सभी मानों का समुच्चय जिनके लिए रैखिक समीकरणों के निकाय
2x1−2x2+x3=λx1
2x1−3x2+2x3=λx2
−x1+2x2=λx3 का एक अतुच्छ हल है,
View Solutionx1+x2≤10,−2x1+3x2≤15x1≥6x1,x2≥0 से सम्बंधित उददेश्य फलन Z=x1+x2 के सुसंगत क्षेत्र का अधिकतम मान है
View Solutionमान X एक याद्द्च्छिक चर है जो मान x1,x2,x3,x4 इस प्रकार ग्रहण करता है कि 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4) चर X का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionमाना कि k एक धनात्मक वास्तविक संख्या है तथा
A=⎡⎢ ⎢⎣2k−12√k2√k2√k1−2k−2√k2k−1⎤⎥ ⎥⎦ एवं B=⎡⎢ ⎢⎣02k−1√k1−2k02√k−√k−2√k0⎤⎥ ⎥⎦
यदि det (adj + A) + det (adj B) = 106, तो [k] का मान है।
[नोट adj M किसी वर्ग आव्यूह M का adjoint तथा [k] अधिकतम पूर्णांक जो k से कम या समान है। ]
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
View Solutionमाना A=⎡⎢⎣2b1bb2+1b1b2⎤⎥⎦ जहाँ b>0 है, तो det(A)b का न्यूतनम मान है
View Solutionयदि x में द्विघात समीकरण 3m2x2+m(m−4)x+2=0 के मुलो का अनुपात λ है तो m का वह न्यूनतम मान जिसके लिए λ+1λ=1 है, है
View Solution
