In normal YDSE experiment maximum intensity is 4I0 in Column I, y-coordinate is given corresponding to centre line In Coloum II resultant intensities are given Match the two columns.
Column IColumn IIAy=λDdp.I=I0By=λD2dq.I=2I0Cy=λD3dr.I=4I0Dy=λD4ds.I=zero
The correct Answer is:A, B, C, D
To solve the problem of matching the y-coordinates with their corresponding resultant intensities in the Young's Double Slit Experiment (YDSE), we will follow these steps:
1. Understanding the Maximum Intensity:
The maximum intensity in the YDSE is given as 4I0. This occurs at the central maximum where the path difference is zero.
2. Phase Difference Calculation:
The phase difference ϕ at any point on the screen can be expressed in terms of the path difference Δx as:
ϕ=2πλΔx
The path difference Δx can be calculated using the formula:
Δx=y⋅dD
where y is the distance from the central maximum, d is the distance between the slits, and D is the distance from the slits to the screen.
3. Intensity Formula:
The resultant intensity I at any point on the screen is given by:
I=4I0cos2(ϕ2)
4. Evaluate Each Case:
We will evaluate the intensity for each y-coordinate given in Column I.
- Case A: y=λDd
- Path difference: Δx=λDd
- Phase difference: ϕ=2π
- Intensity:
I=4I0cos2(π)=4I0⋅1=4I0
- Case B: y=λD2d
- Path difference: Δx=λD2d
- Phase difference: ϕ=π
- Intensity:
I=4I0cos2(π2)=4I0⋅0=0
- Case C: y=λD3d
- Path difference: Δx=λD3d
- Phase difference: ϕ=2π3
- Intensity:
I=4I0cos2(π3)=4I0⋅(12)2=4I0⋅14=I0
- Case D: y=λD4d
- Path difference: Δx=λD4d
- Phase difference: ϕ=π2
- Intensity:
I=4I0cos2(π4)=4I0⋅(1√2)2=4I0⋅12=2I0
5. Matching Columns:
Now we can match the results from Column I with Column II:
- A: y=λDd→I=4I0 (matches with r)
- B: y=λD2d→I=0 (matches with s)
- C: y=λD3d→I=I0 (matches with p)
- D: y=λD4d→I=2I0 (matches with q)
Final Matching:
- A → r
- B → s
- C → p
- D → q
The maximum intensity in the YDSE is given as 4I0. This occurs at the central maximum where the path difference is zero.
The phase difference ϕ at any point on the screen can be expressed in terms of the path difference Δx as:
ϕ=2πλΔx
The path difference Δx can be calculated using the formula:
Δx=y⋅dD
where y is the distance from the central maximum, d is the distance between the slits, and D is the distance from the slits to the screen.
The resultant intensity I at any point on the screen is given by:
I=4I0cos2(ϕ2)
We will evaluate the intensity for each y-coordinate given in Column I.
- Path difference: Δx=λDd
- Phase difference: ϕ=2π
- Intensity:
I=4I0cos2(π)=4I0⋅1=4I0
- Path difference: Δx=λD2d
- Phase difference: ϕ=π
- Intensity:
I=4I0cos2(π2)=4I0⋅0=0
- Path difference: Δx=λD3d
- Phase difference: ϕ=2π3
- Intensity:
I=4I0cos2(π3)=4I0⋅(12)2=4I0⋅14=I0
- Path difference: Δx=λD4d
- Phase difference: ϕ=π2
- Intensity:
I=4I0cos2(π4)=4I0⋅(1√2)2=4I0⋅12=2I0
Now we can match the results from Column I with Column II:
- A: y=λDd→I=4I0 (matches with r)
- B: y=λD2d→I=0 (matches with s)
- C: y=λD3d→I=I0 (matches with p)
- D: y=λD4d→I=2I0 (matches with q)
- A → r
- B → s
- C → p
- D → q
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - medical entrances
42 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE main (Only one option is Correct )
22 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion reason
8 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
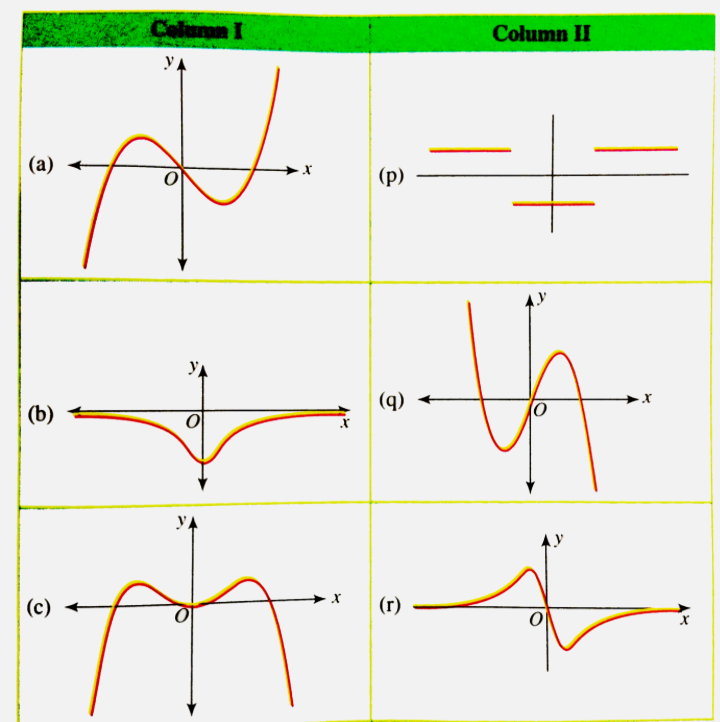
Match the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.

View SolutionMatch column I to columan II according to the given condition
In column I the direction ratios of lines are given. In column II angle between them is given.
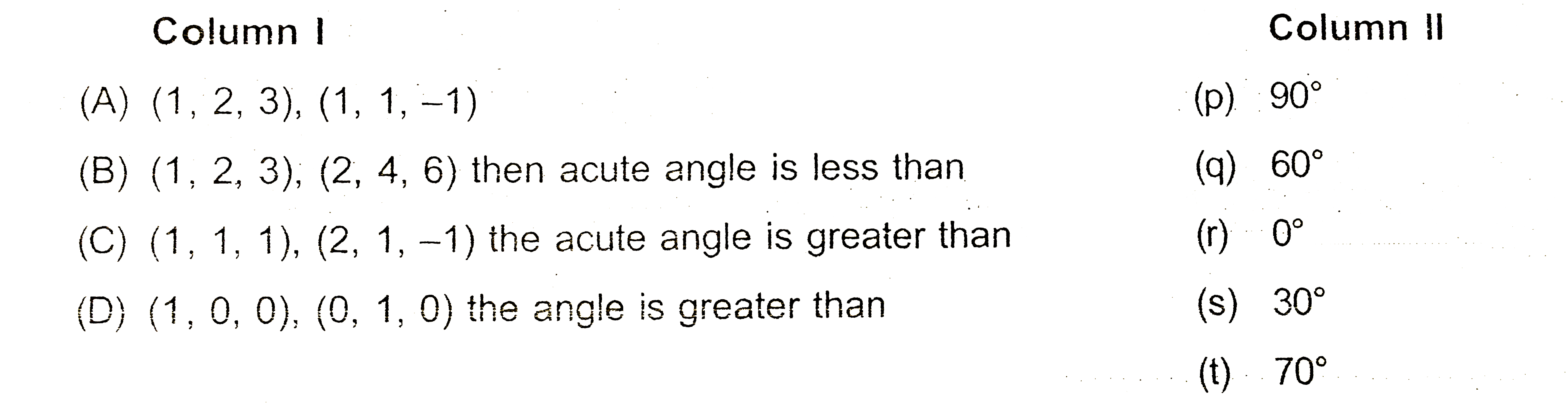
View SolutionMatch the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionMatch the elements given in column (I) with the most appropriate expected values given in column (II)
Column IColumn IIElementElectronegative valuesA.F(p)3.5B.O(q)3.0C.N(r)4.0D.C(s)2.5
View SolutionColumn IColumn II(A)R/L(p)Time(B)C/R(q)Frequency(C)E/B(r)Speed(D)√ε0μ0(s)None
View SolutionMatch column I with column II and select the correct option from the given codes
Column IColumn IIA.Autopolyploidy(i)2n+1B.Trisomy(ii)AAAAC.Allopolyploidy(iii)AABBD.Nullisomy(iv)2n-2
View SolutionMatch the terms in column I with those in column II .
Column IColumn IIA.TrypsinPancreasB.AmylaseLiverC.BileGastric glandsD.PepsinSaliva
View SolutionMatch the column I and II
Column IColumn II(a) Apocarpous(i) Papaver(b) Syncarpous(ii) Michellia(c) Epiphyllous(iii) Cashew(d) Cotyledon(iv) Aloe
View SolutionMatch the Xenon compounds Column-I with its structure in Column-II and assign the correct code :
Column-IColumn-II(a)XeF4(i)pyramidal(b)XeF6(ii) square planar(c)XeOF4(iii) distored octahedral(d)XeO3(iv) square pyramidal
View SolutionMatch the column
Column-IColumn-II(i)MoO+22(A)Alcoholic dehydrogenase(ii)Mg+2(B)Nitrogenase(iii)Zn+2(C)Catalase(iv)Fe+3(D)PEP carboxylase
View Solution
