Bichromatic light is used in YDSE having wavelengths λ1=400nm and λ2=700nm Find minimum order of λ1 which overlaps with λ2
To solve the problem of finding the minimum order of wavelength λ1=400nm that overlaps with wavelength λ2=700nm in Young's Double Slit Experiment (YDSE), we can follow these steps:
Step 1: Understanding the Condition for Overlap
In YDSE, the condition for the bright fringes to overlap is given by the formula:
n1n2=λ2λ1
where n1 is the order of the fringe for λ1 and n2 is the order of the fringe for λ2.
Step 2: Substitute the Wavelengths
Substituting the given wavelengths into the formula:
n1n2=700nm400nm=74
Step 3: Expressing the Orders
From the ratio n1n2=74, we can express n1 in terms of n2:
n1=74n2
Step 4: Finding Integer Values
To find the minimum integer values for n1 and n2, we can set n2=4k for some integer k. Then:
n1=7k
Step 5: Finding the Minimum Order
To find the minimum order, we can take k=1:
n2=4andn1=7
Thus, the minimum order of λ1 that overlaps with λ2 is:
7
In YDSE, the condition for the bright fringes to overlap is given by the formula:
n1n2=λ2λ1
where n1 is the order of the fringe for λ1 and n2 is the order of the fringe for λ2.
Substituting the given wavelengths into the formula:
n1n2=700nm400nm=74
From the ratio n1n2=74, we can express n1 in terms of n2:
n1=74n2
To find the minimum integer values for n1 and n2, we can set n2=4k for some integer k. Then:
n1=7k
To find the minimum order, we can take k=1:
n2=4andn1=7
7
Topper's Solved these Questions
Similar Questions
Bichromatic light is used in YDSE having wavelengths
λ1=400nmandλ2=700nm. Find minimum order of bright fringe of λ1
which overlaps with bright fringe of λ2 .
View SolutionBichromatic light of wavelengths λ1=5000Åandλ2=7000Å are used in YDSE. Then,
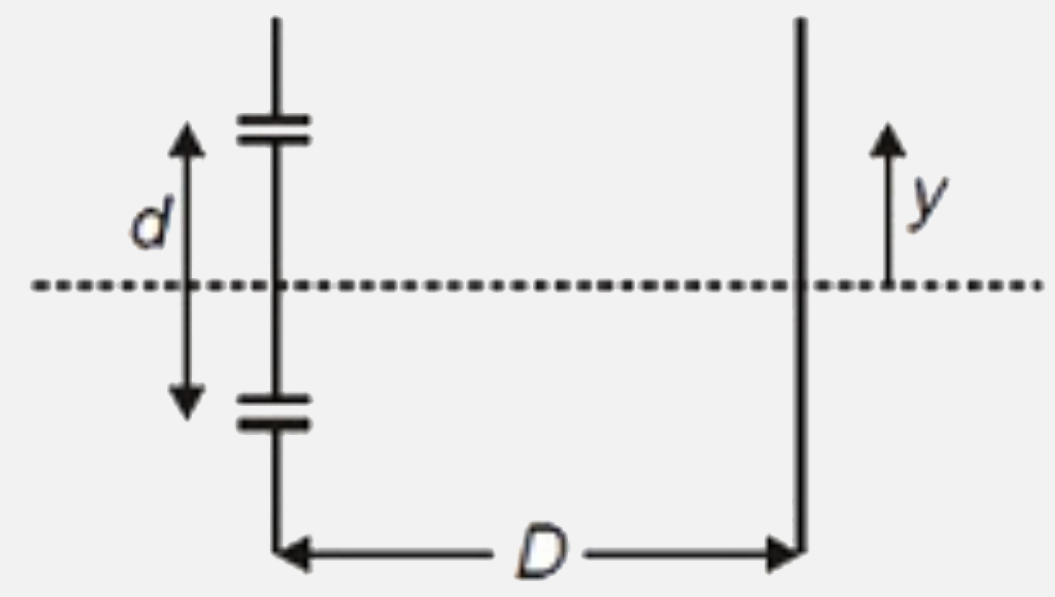
View SolutionIn YDSE, if a bichromatic light having wavelengths λ1 and λ2 is used, then maxima due to both lights will overlaps at a certain distance y from the central maxima. Take separation between slits as d and distance between screen and slits as D. Then the value of y will be
View SolutionIn YDSE a parallel beam of incident light consists of two wavelengths λ1=4000Åandλ2=5600Å. The minimum distance y on the screen, measured from the central axis, where the bright fringe due to two wavelengths coincide is nλ1Dd. Find n.
View SolutionA lens of focal length 1m forms Fraunhofer diffraction pattern of a single slit of width 0.04cm in its focal plane. The incident light contains two wavelength λ1 and λ2. It is found that the fourth minimum corresponding to λ1 and the fifth minimum corresponding to λ2 occur at the same point 0.5cm from the central maximum. Compute λ1 and λ2
View SolutionA double-slit interference pattern is formed on a screen in a Young's double slit experiment performed with light consisting of two wavelengths λ1 = 6000A and λ2 = 4800A. It is observed that the maximum of the 16th order corresponding to λ= 6000 A coincides with a maximum of the n order corresponding to λ= 4800 A The value of n is
View SolutionWavelength of light used in an optical instrument are λ1=4000Å and λ2=5000Å then ratio of their respective resolving powers (corresponding to λ1 and λ2) is
View SolutionA dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View SolutionIf an interference experiment is performed using two wavelengths close to each other, two interference patterns corresponding to the two wavelengths are obtained on the screen. The frings system remains distinct up to a point on the screen where the nth order maximum of one wavelength falls on the nth order minimum of the other wavelength. Suppose in Young's double sit experiment, sodium light composed of two wavelengths λ1andλ2 close to each other (with λ2 greater than λ1) is used. The order n, up to which the fringes can be seen on the screen, is given by
View SolutionThe ratio of resolving power of an optical microscope for two wavelength λ1=4000Å and λ2=6000Å is:
View Solution
