The average power is dissipated in a pure inductor is
VI24
12VI
zero
VI2
The correct Answer is:C
To solve the question regarding the average power dissipated in a pure inductor, we can follow these steps:
1. Understanding the Circuit: In a pure inductive circuit, the current lags behind the voltage by 90 degrees (or π/2 radians). This is a fundamental characteristic of inductors in AC circuits.
2. Identifying the Phase Difference: The phase difference (φ) between the voltage and current in a pure inductor is given as:
ϕ=90∘
3. Using the Power Formula: The average power (P) in an AC circuit can be calculated using the formula:
P=VrmsIrmscosϕ
where Vrms is the root mean square voltage, Irms is the root mean square current, and cosϕ is the cosine of the phase difference.
4. Calculating Cosine of the Phase Difference: Since we have a phase difference of 90 degrees:
cos90∘=0
5. Substituting into the Power Formula: Now substituting the value of cosϕ into the power formula:
P=VrmsIrms⋅0=0
6. Conclusion: Therefore, the average power dissipated in a pure inductor is:
P=0
Final Answer:
The average power dissipated in a pure inductor is 0.
ϕ=90∘
P=VrmsIrmscosϕ
where Vrms is the root mean square voltage, Irms is the root mean square current, and cosϕ is the cosine of the phase difference.
cos90∘=0
P=VrmsIrms⋅0=0
P=0
The average power dissipated in a pure inductor is 0.
Similar Questions
Knowledge Check
Assertion : In a purely inductive or capacitive circuit, the current is referred to as wattless currents.
Reason : No power is dissipated in a purely inductive or capacitive circuit even though a current is flowing in the circuit.AIf both assertion ans reason are true ans reaason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion istrue but reason is false.DIf both assertion and reason are false.
Power dissipated in pure inductance will be-
View SolutionIn the circuit shown, the average power dissipated in the resistor is (assume diode to be ideal)
View SolutionThe voltage E and the current I in an instrument are represented by the equations:
E=2cosωtV
I=2sinωtA
The average power dissipated in the instrument will be
View SolutionA 10 ohm resistor is conneted to a supply voltage alternating between +4V and -2V as shown in the following graph. The average power dissipated in the resistor per cycle is
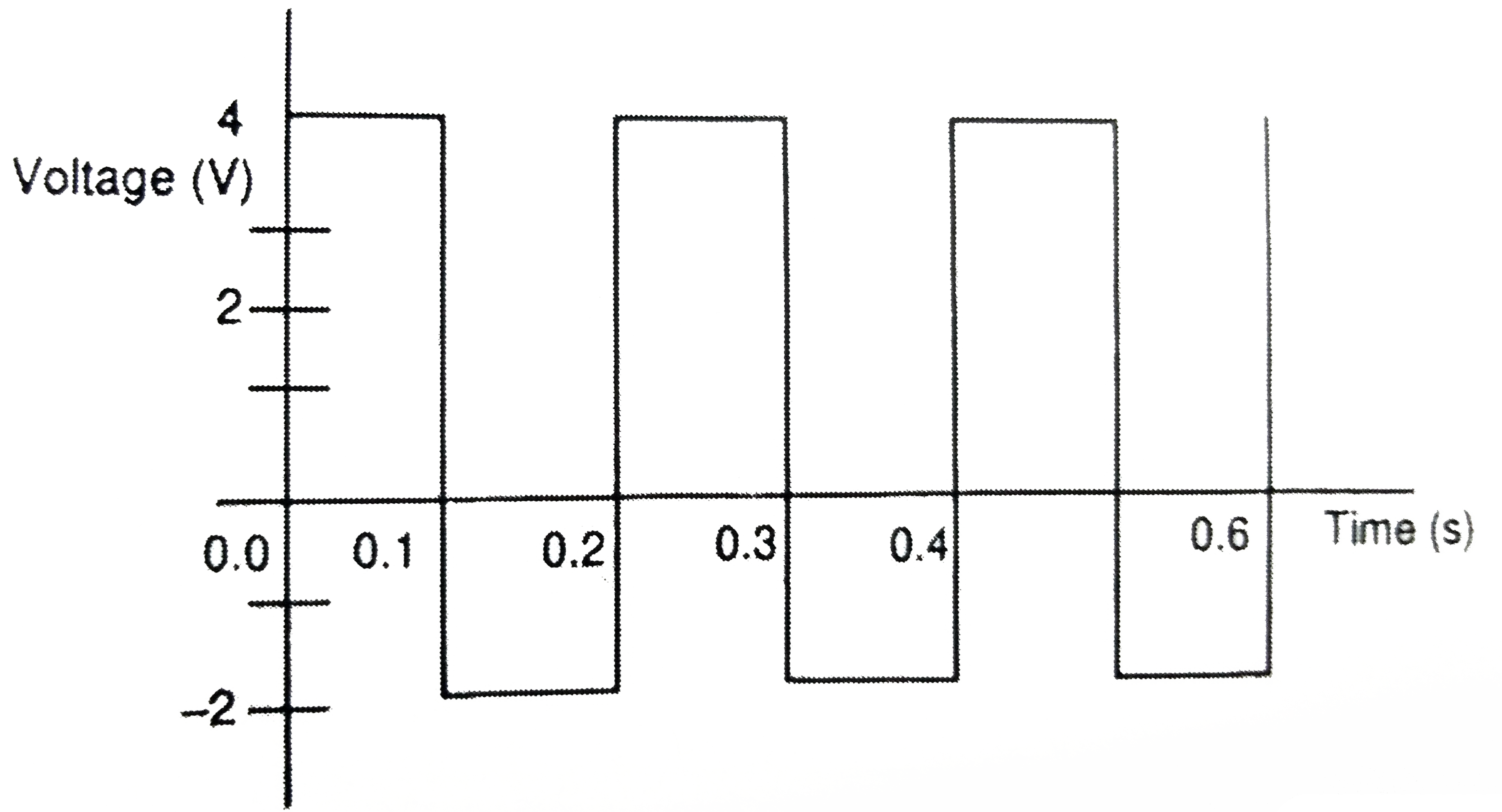
View SolutionIn a series LCR circuit, an alternating emf (V) and current (I) are given by the equation V=V0sinωt,I=I0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
View SolutionThe average power dissipated in AC circuit is 2W. If a current flowing throuh a circuit is 2A, impedance is 1Ω, then what is the power factor of the circuit?
View SolutionA capacitor of capacitance 2 mF and resistor of resistance 12 Ω are connected in series with voltage source V=(195√2(V))[sin(100rads)t] - The average power dissipated in the circuit will be
View Solution
