The phase difference between the flux linkage and the induced e.m.f. in a rotating coil in a uniform magnetic field
The correct Answer is:A
To solve the problem of finding the phase difference between the flux linkage and the induced e.m.f. in a rotating coil in a uniform magnetic field, we can follow these steps:
1. Understand the Flux Linkage:
The magnetic flux (Φ) linked with a coil rotating in a uniform magnetic field can be expressed as:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the coil.
2. Express the Angle in Terms of Time:
If the coil is rotating with an angular velocity ω, the angle θ can be expressed as:
θ=ωt
Thus, the flux can be rewritten as:
Φ=B⋅A⋅cos(ωt)
3. Calculate the Induced e.m.f.:
The induced e.m.f. (ε) in the coil can be found using Faraday's law of electromagnetic induction, which states:
ε=−dΦdt
Substituting the expression for flux:
ε=−ddt(B⋅A⋅cos(ωt))
4. Differentiate the Flux:
Using the chain rule to differentiate:
ε=−B⋅A⋅ddt(cos(ωt))=−B⋅A⋅(−ωsin(ωt))
Simplifying gives:
ε=B⋅A⋅ωsin(ωt)
5. Identify the Phase of Flux and e.m.f.:
The expressions for flux and induced e.m.f. are:
- Flux: Φ=B⋅A⋅cos(ωt)
- Induced e.m.f.: ε=B⋅A⋅ωsin(ωt)
The cosine function can be expressed in terms of sine:
cos(ωt)=sin(ωt+π2)
This shows that the flux is leading the induced e.m.f. by π2.
6. Calculate the Phase Difference:
The phase difference (Δϕ) between the flux linkage and the induced e.m.f. is given by:
Δϕ=(ωt+π2)−ωt=π2
Final Answer:
The phase difference between the flux linkage and the induced e.m.f. in a rotating coil in a uniform magnetic field is π2.
---
The magnetic flux (Φ) linked with a coil rotating in a uniform magnetic field can be expressed as:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the coil.
If the coil is rotating with an angular velocity ω, the angle θ can be expressed as:
θ=ωt
Thus, the flux can be rewritten as:
Φ=B⋅A⋅cos(ωt)
The induced e.m.f. (ε) in the coil can be found using Faraday's law of electromagnetic induction, which states:
ε=−dΦdt
Substituting the expression for flux:
ε=−ddt(B⋅A⋅cos(ωt))
Using the chain rule to differentiate:
ε=−B⋅A⋅ddt(cos(ωt))=−B⋅A⋅(−ωsin(ωt))
Simplifying gives:
ε=B⋅A⋅ωsin(ωt)
The expressions for flux and induced e.m.f. are:
- Flux: Φ=B⋅A⋅cos(ωt)
- Induced e.m.f.: ε=B⋅A⋅ωsin(ωt)
cos(ωt)=sin(ωt+π2)
This shows that the flux is leading the induced e.m.f. by π2.
The phase difference (Δϕ) between the flux linkage and the induced e.m.f. is given by:
Δϕ=(ωt+π2)−ωt=π2
The phase difference between the flux linkage and the induced e.m.f. in a rotating coil in a uniform magnetic field is π2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
The induced e.m.f. in a coil does not depend on
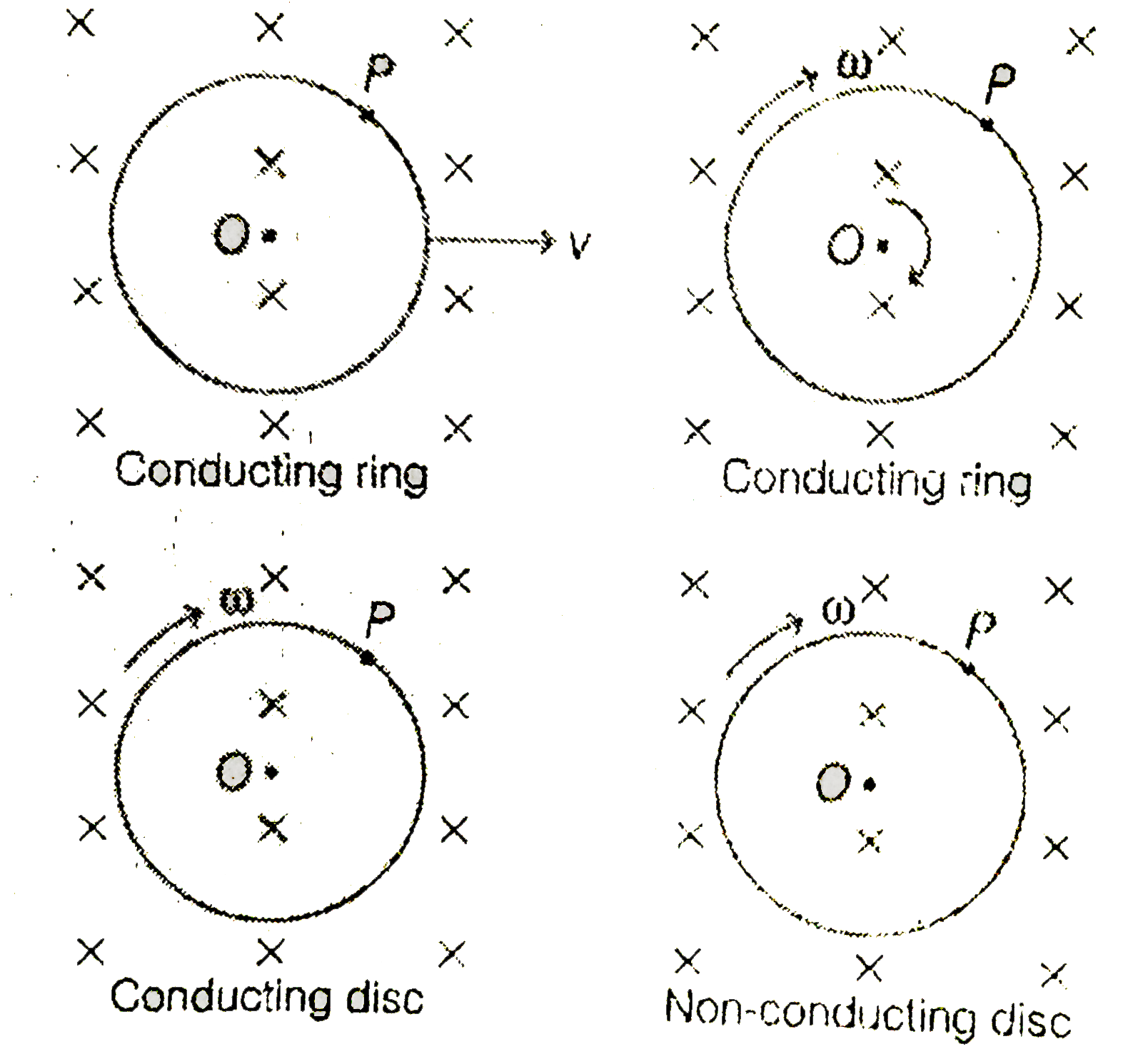
View SolutionSome cases are given below. Identify the case in which emf is induced between O and P in uniform magnetic field
View SolutionTwo identical coils, one of copper and the other of iron, are rotated with the same angular velocity ω in a uniform magnetic field. In which case the induced e.m.f. is more and why?
View SolutionAssertion If a loop is placed in a non-uniform (with respect to position) magnetic field, then induced emf is produced in the loop.
Reason In a non-uniform magnetic field, magnetic flux passing through the loop will change. Therefore, induced emf is produced.
View SolutionA square coil of side 25cm having 1000 turns is rotated with a uniform speed in a magnetic field about axis perpendicular to the direction of the field. At an instant t, the e.m.f. induced in the coil is e=200sin100πt. The magnetic induction is
View SolutionThe magnetic flux linked with a coil (in Wb) is given by the equation ϕ=5t2+3t+16 . The magnetic of induced emf in the coil at fourth second will be
View SolutionA rectangular coil rotates about an axis normal to the magnetic field, If Em is the maximum value of the induced emf, then the instantaneous emf when plane of the coil makes an angle of 45∘ with the magnetic field is
View SolutionA square coil of 100 turns and side length 1 cm is rotating in a uniform magnetic field such that axis of rotation is perpendicular to magnetic field. If coil completes 1 rotation in 1ms.Find average EMF induced in μV) in half rotation. ( Magnetic field (B)=10−5T ) .
View SolutionA square coil of 100 turns and side length 1 cm is rotating in a uniform magnetic field such that axis of rotation is perpendicular to magnetic field. If coil completes 1 rotation in 1ms.Find average EMF induced in μV) in half rotation. ( Magnetic field (B)=10−5T ) .
View SolutionThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
View Solution
