A thin rectangular magnet suspended freely has a period of oscillation equal to T. Now it is broken into two equal halves (each having half of the original length) and one piece is made to oscillate freely in the same field. If its period of oscillation is T′, then ratio T′T is
To solve the problem, we need to analyze the changes in the time period of oscillation when a rectangular magnet is cut in half. The time period of a magnet oscillating in a magnetic field can be expressed using the formula:
T=2π√ImB
where:
- T is the time period of oscillation,
- I is the moment of inertia,
- m is the mass of the magnet,
- B is the magnetic field strength.
Step 1: Determine the moment of inertia of the original magnet
For a thin rectangular magnet of length L and mass m0, the moment of inertia I about its center is given by:
I=m0L212
Step 2: Analyze the changes when the magnet is cut in half
When the magnet is cut into two equal halves:
- Each half will have a length of L2 and a mass of m02.
Step 3: Calculate the moment of inertia of one half
The moment of inertia I′ for one half of the magnet is:
I′=(m02)(L2)212=m02⋅L24⋅112=m0L296
Step 4: Write the expression for the new time period T′
The new time period T′ for one half of the magnet is:
T′=2π√I′m′B=2π
⎷m0L296m02B=2π√L248B
Step 5: Compare the new time period T′ with the original time period T
The original time period T was:
T=2π√ImB=2π
⎷m0L212m0B=2π√L212B
Step 6: Find the ratio T′T
Now, we can find the ratio T′T:
T′T=2π√L248B2π√L212B=
⎷L248BL212B=√1248=√14=12
Conclusion
Thus, the ratio of the new time period T′ to the original time period T is:
T′T=12
- T is the time period of oscillation,
- I is the moment of inertia,
- m is the mass of the magnet,
- B is the magnetic field strength.
For a thin rectangular magnet of length L and mass m0, the moment of inertia I about its center is given by:
When the magnet is cut into two equal halves:
- Each half will have a length of L2 and a mass of m02.
The moment of inertia I′ for one half of the magnet is:
The new time period T′ for one half of the magnet is:
⎷m0L296m02B=2π√L248B
The original time period T was:
⎷m0L212m0B=2π√L212B
Now, we can find the ratio T′T:
⎷L248BL212B=√1248=√14=12
Thus, the ratio of the new time period T′ to the original time period T is:
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - 5.1
15 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - 5.2
15 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now T2. The ratio of T2/T1 is
View SolutionA uniform spring has a centain block suspended from it and its period for vertical oscillation is T1. The spring is now cut into two parts of lengths 13rdand23rd of original length and these springs are connected to the same block as shown in the figure. If time period of oscillation now is T2 then T1/T2.

View SolutionOne mass m is suspended from a spring. Time period of oscilation is T. now if spring is divided into n pieces & these are joined in parallel order then time period of oscillation if same mass is suspended.
View SolutionIf the same weight is suspended from three springs having length in the ratio 1 : 3 : 5 , the period of oscillations shall be the ratio of
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA thin magnetic needle oscillates in a horizontal plane with a period T. It is broken into n equals parts. The time period of each part will be
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
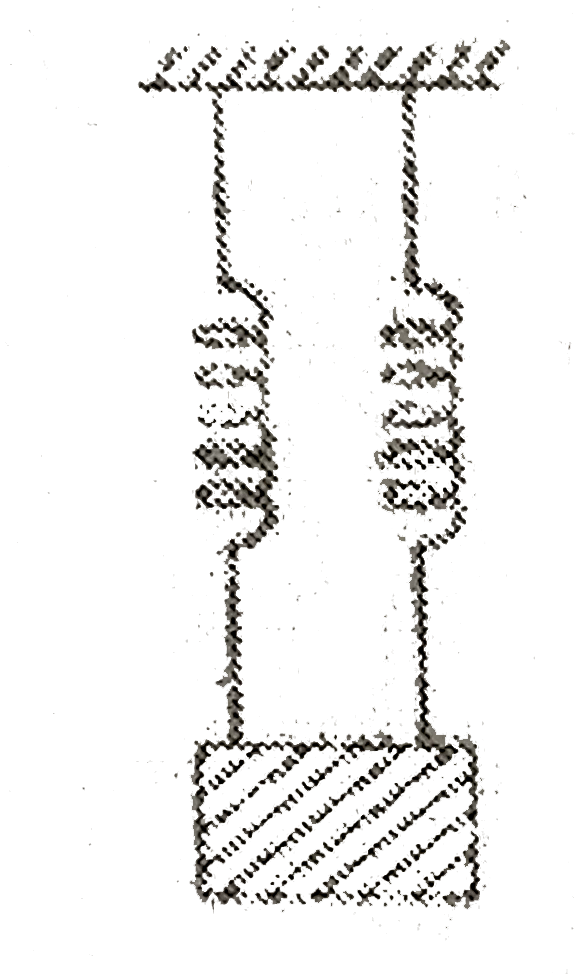
View SolutionA pendulum is suspended in a ligt and its period of oscillation when the lift is stationary is Ta. What must be the accleraion of the lift for the period of oscillation of the pendulum to be T0/2?
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View Solution
