A load suspended by a massless spring produces an extention of xcm in equilibrium.When it is cut into two unequal parts ,the same load produces an extention of 7.5cm when suspended by the larger part of length 60cm .When it is suspended by the smaller part,the extention is 5cm.Then
x=12.5cm
x=3.0cm
the length of the original spring is 90cm
the length of the original spring is 80cm
The correct Answer is:A
To solve the problem step-by-step, we will follow the principles of elasticity and the relationships between force, extension, and length of the spring.
Step 1: Understand the Problem
We have a spring that produces an extension x cm when a load is suspended from it. The spring is then cut into two unequal parts. The larger part (length = 60 cm) produces an extension of 7.5 cm, and the smaller part produces an extension of 5 cm.
Step 2: Set Up the Relationships
According to Hooke's Law, the extension produced in a spring is directly proportional to the load applied and the original length of the spring. Therefore, we can write:
ΔL1ΔL2=L1L2
Where:
- ΔL1 is the extension of the smaller part (5 cm).
- ΔL2 is the extension of the larger part (7.5 cm).
- L1 is the length of the smaller part.
- L2 is the length of the larger part (60 cm).
Step 3: Calculate the Length of the Smaller Part
Let L1 be the length of the smaller part. We know L2=60 cm and ΔL2=7.5 cm. Plugging in the values:
57.5=L160
Cross-multiplying gives:
5×60=7.5×L1
300=7.5×L1
Now, solving for L1:
L1=3007.5=40 cm
Step 4: Find the Total Length of the Spring
The total length of the original spring L0 is the sum of the lengths of the two parts:
L0=L1+L2=40 cm+60 cm=100 cm
Step 5: Calculate the Original Extension x
Now we can find the original extension x when the entire spring of length 100 cm is used. Using the same ratio of extensions:
xΔL2=L0L2
Substituting the known values:
x7.5=10060
Cross-multiplying gives:
x×60=7.5×100
60x=750
Now, solving for x:
x=75060=12.5 cm
Final Answer
The original extension x of the spring is 12.5 cm.
---
We have a spring that produces an extension x cm when a load is suspended from it. The spring is then cut into two unequal parts. The larger part (length = 60 cm) produces an extension of 7.5 cm, and the smaller part produces an extension of 5 cm.
According to Hooke's Law, the extension produced in a spring is directly proportional to the load applied and the original length of the spring. Therefore, we can write:
- ΔL1 is the extension of the smaller part (5 cm).
- ΔL2 is the extension of the larger part (7.5 cm).
- L1 is the length of the smaller part.
- L2 is the length of the larger part (60 cm).
Let L1 be the length of the smaller part. We know L2=60 cm and ΔL2=7.5 cm. Plugging in the values:
The total length of the original spring L0 is the sum of the lengths of the two parts:
Now we can find the original extension x when the entire spring of length 100 cm is used. Using the same ratio of extensions:
The original extension x of the spring is 12.5 cm.
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.3
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A block of weight W produces an extension of 9cm when it is hung by an elastic spring of length of 60cm and is in equilibrium. The spring is cut into two parts, one of length 40cm and the other of length 20cm. The same load W hangs in equilibrium supported by both parts as shwon in figure. The extension in cm noe is
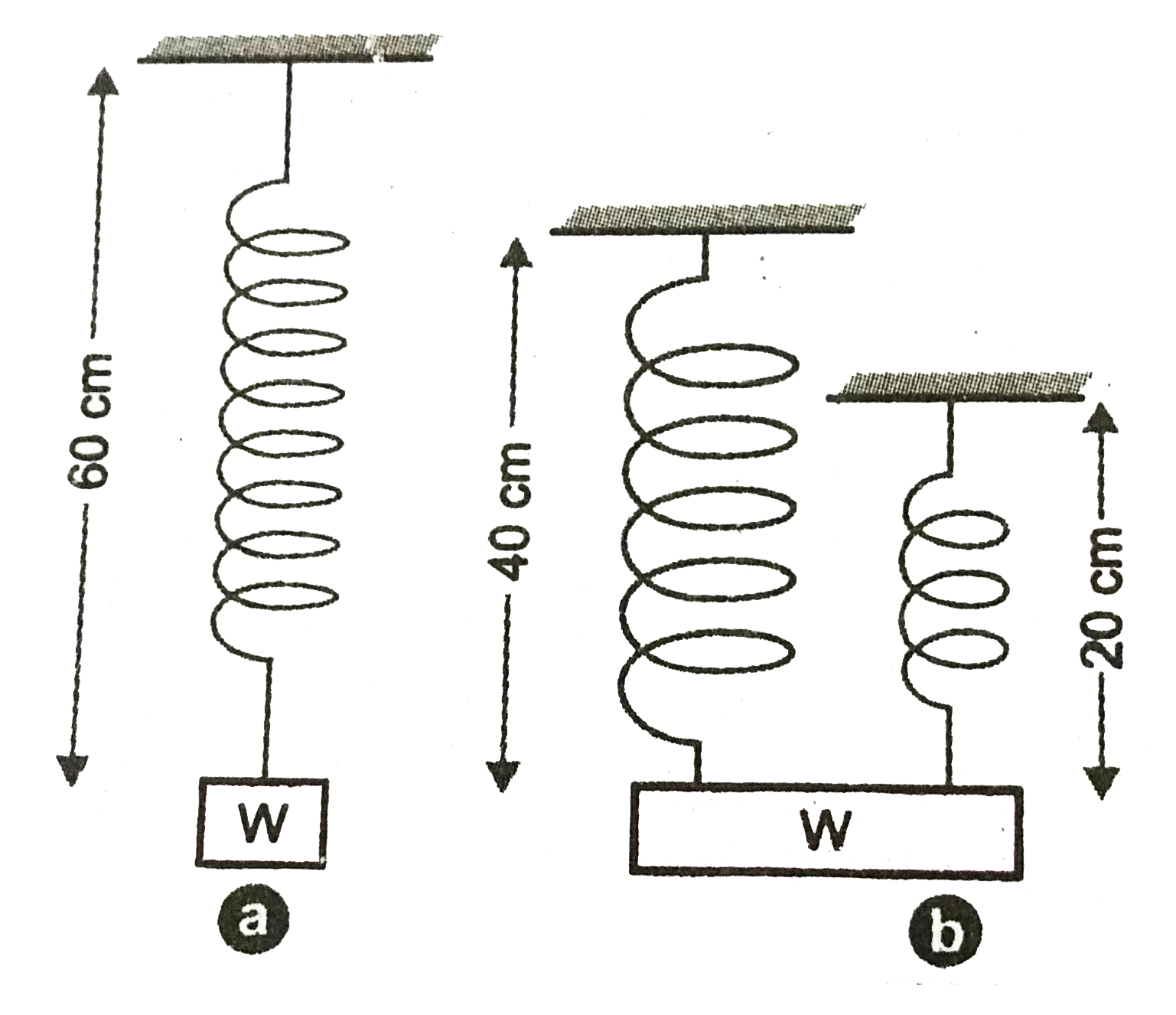
View SolutionA block of weight W produces an extension of 9cm when it is hung by an elastic spring of length of 60cm and is in equilibrium. The spring is cut into two parts, one of length 40cm and the other of length 20cm. The same load W hangs in equilibrium supported by both parts as shwon in figure. The extension in cm noe is

View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionOne body is suspended from a spring of length l, spring constant k and has time period T, Now if spring is divided in two equal parts which are joined in paralled and the same body is suspended from this arrangements then determine new time period.
View SolutionPotential energy of an ideal spring, when stretched by 1 cm is U. Spring is now cut in two equal parts and connected in parallel. If the new combination of spring is compressed by 2 cm, then potential energy stored is
View SolutionA pole of length 1 m 80 cm is divided into two parts such that their lengths are in the ratio 5:7. Find the length of each part of the pole.
View SolutionTwo masses m1andm2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is
View SolutionTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
View SolutionTwo masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is

View Solution
