On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).

sin−1(u23gR+23)
cos−1(u23gR+23)
cos−1(u26gR+43)
sin−1(u26gR+23)
h=R−Rcosθ
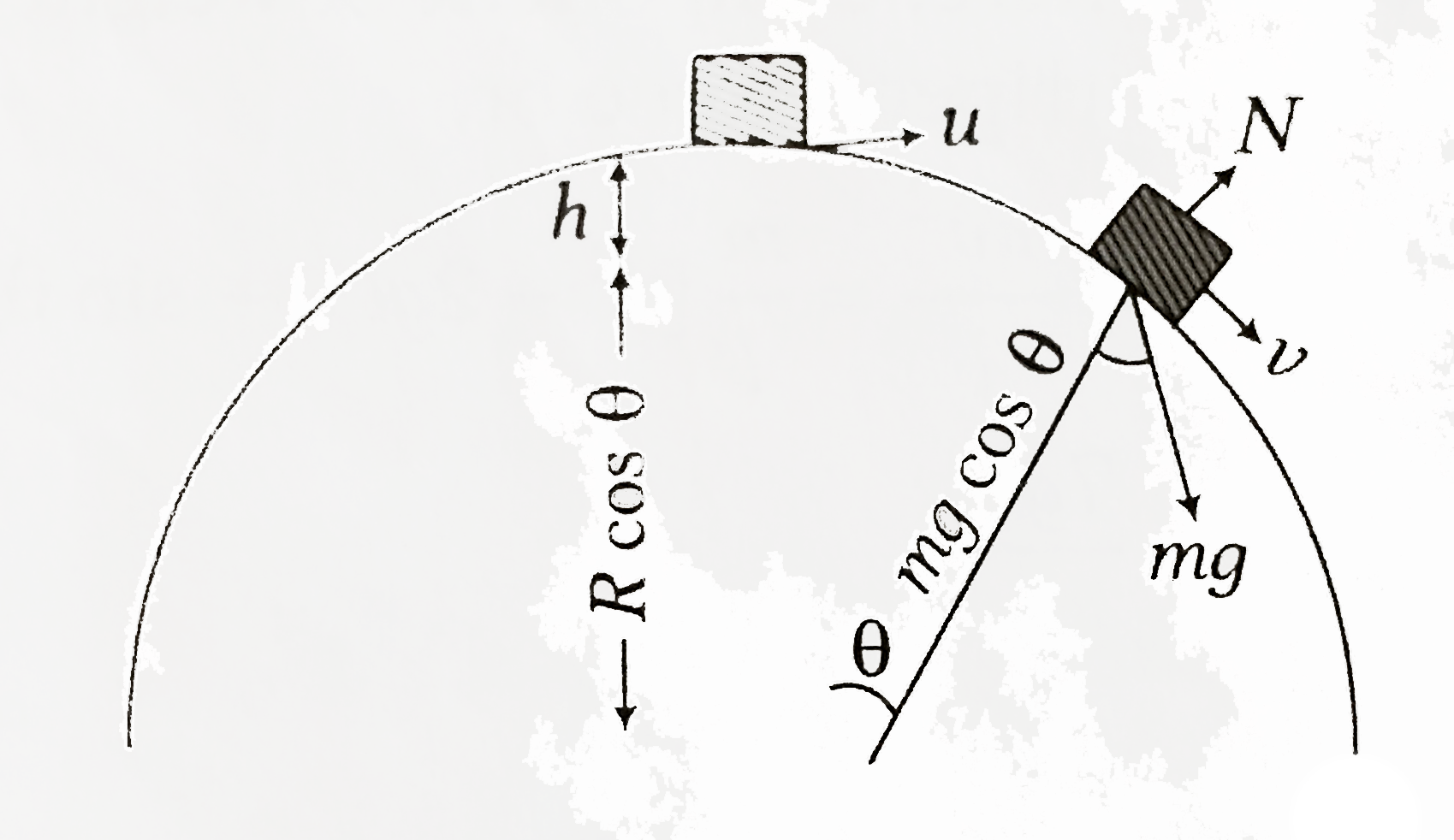
v2=u2+2gh=u2+2gR(1−cosθ) ….(i)
mgcosθ−N=mv2R ….(ii)
When the particle loses contact
N = 0 ….(iii)
From Eqs. (i), (ii) and (iii), we have
⇒ v2=gRcosθ=u2+2gR(1−cosθ)
⇒ 3gRcosθ=u2+2gR
⇒ cosθ=u23gR+23
⇒ θ=cos−1(u23gR+23)
Similar Questions
Knowledge Check
A line makes an angle π4 with each y-axis and z-axis. The angle that it makes with the x - axis is
Aπ2Bπ4CπDπ6
A vector lying in x-y plane has a magnitude 3, and makes an angle 30∘ with the x-axis. Find its components along the two axes.
View SolutionA line makes an angle of 600 with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
View SolutionA line makes an angle of 600 with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
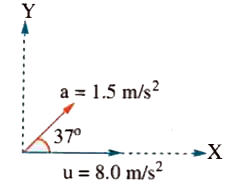
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionFind the equation of the straight line which cuts off an intercept-5 from the y-axis and makes an angle of sin−1(1213) with the x-axis.
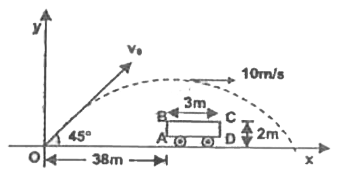
View SolutionA ball is thrown from the origin in the x-y plane with velocity 28.28m/s at an angle of 45∘ with x-axis.At the same instant a trolley also starts moving with uniform velocity of 10m/s along the positive x-axis . Initially , the trolley is located at 38m from the origin. Determine the time at which the ball hits the trolley.
View Solution

