Find the voltage across the various elements, i.e., resistance, capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H, respectively. Given emf is
V=100√2sin1000t volt
To solve the problem of finding the voltage across the various elements in a series circuit consisting of a resistor (R), capacitor (C), and inductor (L), we will follow these steps:
Step 1: Identify the given values
- Resistance, R=1000Ω
- Capacitance, C=1μF=1×10−6F
- Inductance, L=2.0H
- EMF, V=100√2sin(1000t)V
Step 2: Determine the peak voltage and angular frequency
From the given EMF equation, we can identify:
- Peak voltage, V0=100√2
- Angular frequency, ω=1000rad/s
Step 3: Calculate the RMS voltage
The RMS voltage is given by the formula:
Vrms=V0√2
Substituting the value of V0:
Vrms=100√2√2=100V
Step 4: Calculate the reactance of the inductor and capacitor
- Inductive reactance, XL=ωL:
XL=1000×2=2000Ω
- Capacitive reactance, XC=1ωC:
XC=11000×1×10−6=1000Ω
Step 5: Calculate the total impedance
The total impedance Z in a series circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√10002+(2000−1000)2=√10002+10002=√2×10002=1000√2Ω
Step 6: Calculate the RMS current
The RMS current Irms can be calculated using:
Irms=VrmsZ
Substituting the values:
Irms=1001000√2=1001000√2=110√2≈0.0707A
Step 7: Calculate the voltage across the resistor
The voltage across the resistor VR is given by:
VR=Irms×R
Substituting the values:
VR=0.0707×1000=70.7V
Step 8: Calculate the voltage across the inductor
The voltage across the inductor VL is given by:
VL=Irms×XL
Substituting the values:
VL=0.0707×2000=141.4V
Step 9: Calculate the voltage across the capacitor
The voltage across the capacitor VC is given by:
VC=Irms×XC
Substituting the values:
VC=0.0707×1000=70.7V
Final Results
- Voltage across the resistor, VR=70.7V
- Voltage across the inductor, VL=141.4V
- Voltage across the capacitor, VC=70.7V
- Resistance, R=1000Ω
- Capacitance, C=1μF=1×10−6F
- Inductance, L=2.0H
- EMF, V=100√2sin(1000t)V
From the given EMF equation, we can identify:
- Peak voltage, V0=100√2
- Angular frequency, ω=1000rad/s
The RMS voltage is given by the formula:
Vrms=V0√2
Substituting the value of V0:
Vrms=100√2√2=100V
- Inductive reactance, XL=ωL:
XL=1000×2=2000Ω
- Capacitive reactance, XC=1ωC:
XC=11000×1×10−6=1000Ω
The total impedance Z in a series circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√10002+(2000−1000)2=√10002+10002=√2×10002=1000√2Ω
The RMS current Irms can be calculated using:
Irms=VrmsZ
Substituting the values:
Irms=1001000√2=1001000√2=110√2≈0.0707A
The voltage across the resistor VR is given by:
VR=Irms×R
Substituting the values:
VR=0.0707×1000=70.7V
The voltage across the inductor VL is given by:
VL=Irms×XL
Substituting the values:
VL=0.0707×2000=141.4V
The voltage across the capacitor VC is given by:
VC=Irms×XC
Substituting the values:
VC=0.0707×1000=70.7V
- Voltage across the resistor, VR=70.7V
- Voltage across the inductor, VL=141.4V
- Voltage across the capacitor, VC=70.7V
Topper's Solved these Questions
Similar Questions
Find the voltage across the various elements, i.e., resistance, capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0 H respectively . Given emf as,
V = 100sqrt2 sin 1000 t V
View SolutionFind the potential difference across resistance, capacitance and inductance in series LCR circuit where L=2.0H,C=1μFandR=100Ω. The applied emf has the form V=100√2sin(1000t)
View Solution
Knowledge Check
A resistor of 500Ω and an inductance of 0.5 H are in series with an ac source which is given by V=100√2sin(1000t). The power factor of the combination is
A1√2B1√3C0.5D0.6
In the circuit shown E,F,G and H are cells of emf 2V,1V,3V and 1V respectively and their internal resistance are 2Ω,1Ω,3Ω and 1Ω respectively.
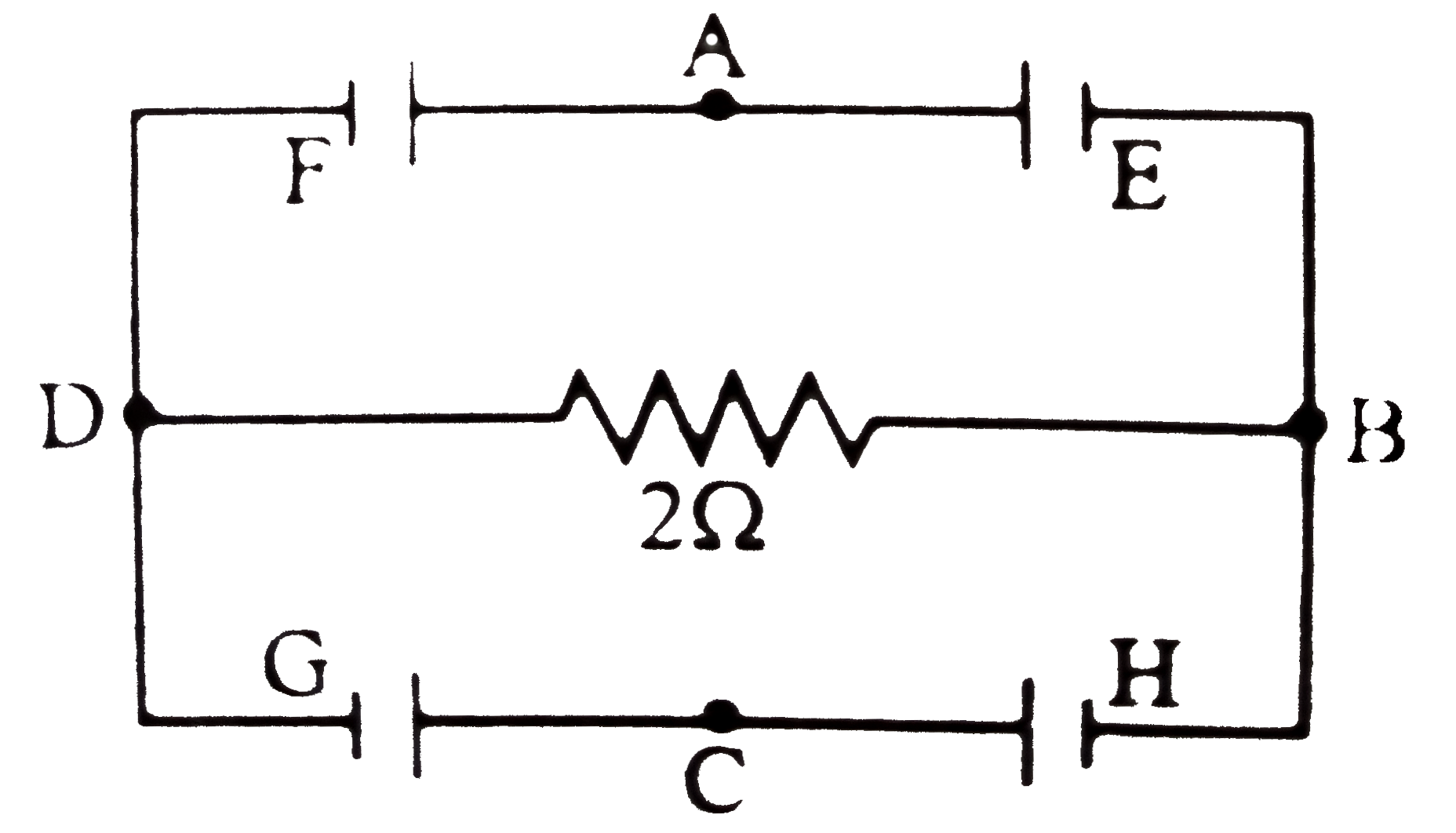
View SolutionIn the circuit shown E,F,G and H are cells of emf 2V,1V,3V and 1V respectively and their internal resistance are 2Ω,1Ω,3Ω and 1Ω respectively.

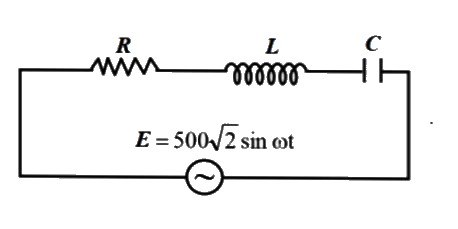
View SolutionIn the series L−C−R circuit shown in the figure, the rms voltage across the resistor and inductor are 400 V and 700 V respectively. If the applied voltage is E=500√2sin(ωt), then the peak voltage across the capacitor is
View SolutionA capacitor of capacitance 100μF and a coil of resistance 50Ω and inductance 0.5H are connected in series with a110V,50HzAC source. Find the rms value of the current.
View SolutionTwo batteries with emf 12 V and 13V are connected in parallel across a load resistor of 10Ω . The internal resistances of the two batteries are 1Ωand2Ω respectively . The voltage across the load lies between
View SolutionA coil having a resistance of 5 Ω and an inductance of 0.02H is arranged in parallel with another coil having a resistance of 1Ω and an inductance of 0.08H. Calculate the power absorbed when a voltage of 100V at 50Hz is applied.
 .
.
View SolutionIn a series RLC circuit the r.m.s. voltage across the resistor and the inductor are respectively 400 V and 700 V. If the equation for the applied Voltage is ε=500√2sinωt. then the peak voltage across the capacitor is

View Solution
