A uniform electric field pointing in positive x-direction exists in a region. Let A be the origin, B be the point on the x-axis at x=+1cm and C be the point on the y-axis at y=+1cm. then the potential at the points A,B and C satisfy
a. VA<VB, b. VA>VB c. VA<VC d. VA>VC
To solve the problem, we need to analyze the potential at points A, B, and C in a uniform electric field pointing in the positive x-direction.
1. Understanding the Electric Field:
The electric field →E is uniform and directed along the positive x-axis. We can represent this as:
→E=E^i
where E is the magnitude of the electric field.
2. Identifying Points:
- Point A is at the origin: (0,0)
- Point B is at (1cm,0) on the x-axis.
- Point C is at (0,1cm) on the y-axis.
3. Electric Potential Difference:
The potential difference between two points in an electric field is given by:
VA−VB=−∫BA→E⋅d→r
Since the electric field is uniform, this simplifies to:
VA−VB=−E⋅(xB−xA)
Here, xA=0 and xB=1cm:
VA−VB=−E⋅(1cm−0)=−E⋅1cm
Thus, we have:
VA=VB+E⋅1cm
4. Comparing Potentials at A and B:
Since E is positive, it follows that:
VA>VB
5. Potential at Point C:
Point C is at (0,1cm). The potential difference between A and C can be calculated similarly:
VA−VC=−∫CA→E⋅d→r
The path from A to C is vertical, and since the electric field is horizontal, the dot product →E⋅d→r will be zero. Therefore:
VA−VC=0⟹VA=VC
6. Final Comparisons:
- From the above calculations, we have:
- VA>VB
- VA=VC
- Thus, we can conclude:
- VA>VB (Option B is correct)
- VA=VC (not an option)
- VB<VC (not directly stated)
Conclusion:
The correct answer is:
- Option B: VA>VB
The electric field →E is uniform and directed along the positive x-axis. We can represent this as:
→E=E^i
where E is the magnitude of the electric field.
- Point A is at the origin: (0,0)
- Point B is at (1cm,0) on the x-axis.
- Point C is at (0,1cm) on the y-axis.
The potential difference between two points in an electric field is given by:
VA−VB=−∫BA→E⋅d→r
Since the electric field is uniform, this simplifies to:
VA−VB=−E⋅(xB−xA)
Here, xA=0 and xB=1cm:
VA−VB=−E⋅(1cm−0)=−E⋅1cm
Thus, we have:
VA=VB+E⋅1cm
Since E is positive, it follows that:
VA>VB
Point C is at (0,1cm). The potential difference between A and C can be calculated similarly:
VA−VC=−∫CA→E⋅d→r
The path from A to C is vertical, and since the electric field is horizontal, the dot product →E⋅d→r will be zero. Therefore:
VA−VC=0⟹VA=VC
- From the above calculations, we have:
- VA>VB
- VA=VC
- Thus, we can conclude:
- VA>VB (Option B is correct)
- VA=VC (not an option)
- VB<VC (not directly stated)
The correct answer is:
- Option B: VA>VB
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
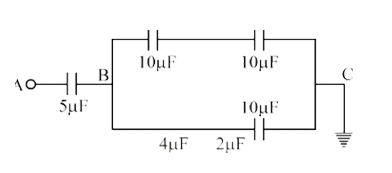
As shown in figure, if the point C is earthed and the point A is given a potential of 2000 V, then the potential at point B will be :
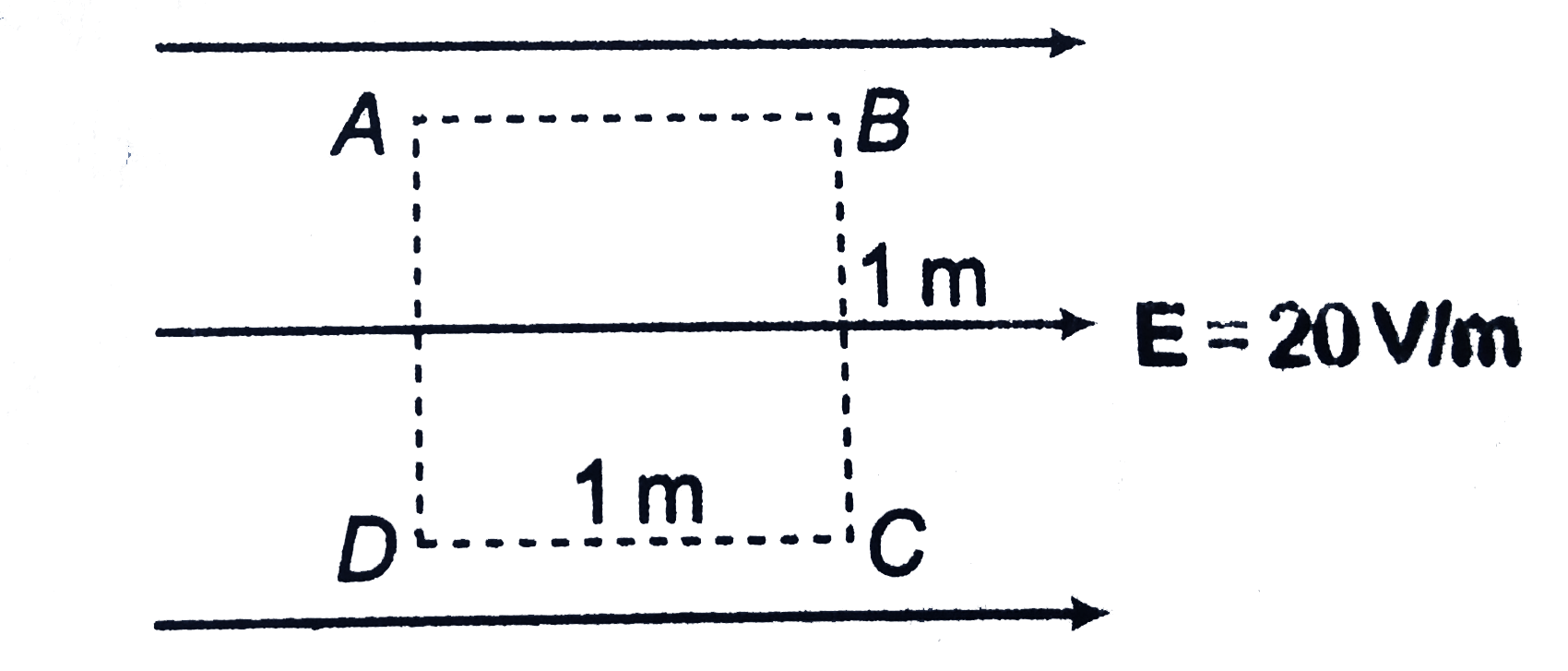
View SolutionIn the uniform electric field shown in figure, find :
a. VA−VD
b. VA−VC
c. VB−VD
d. VC−VD
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
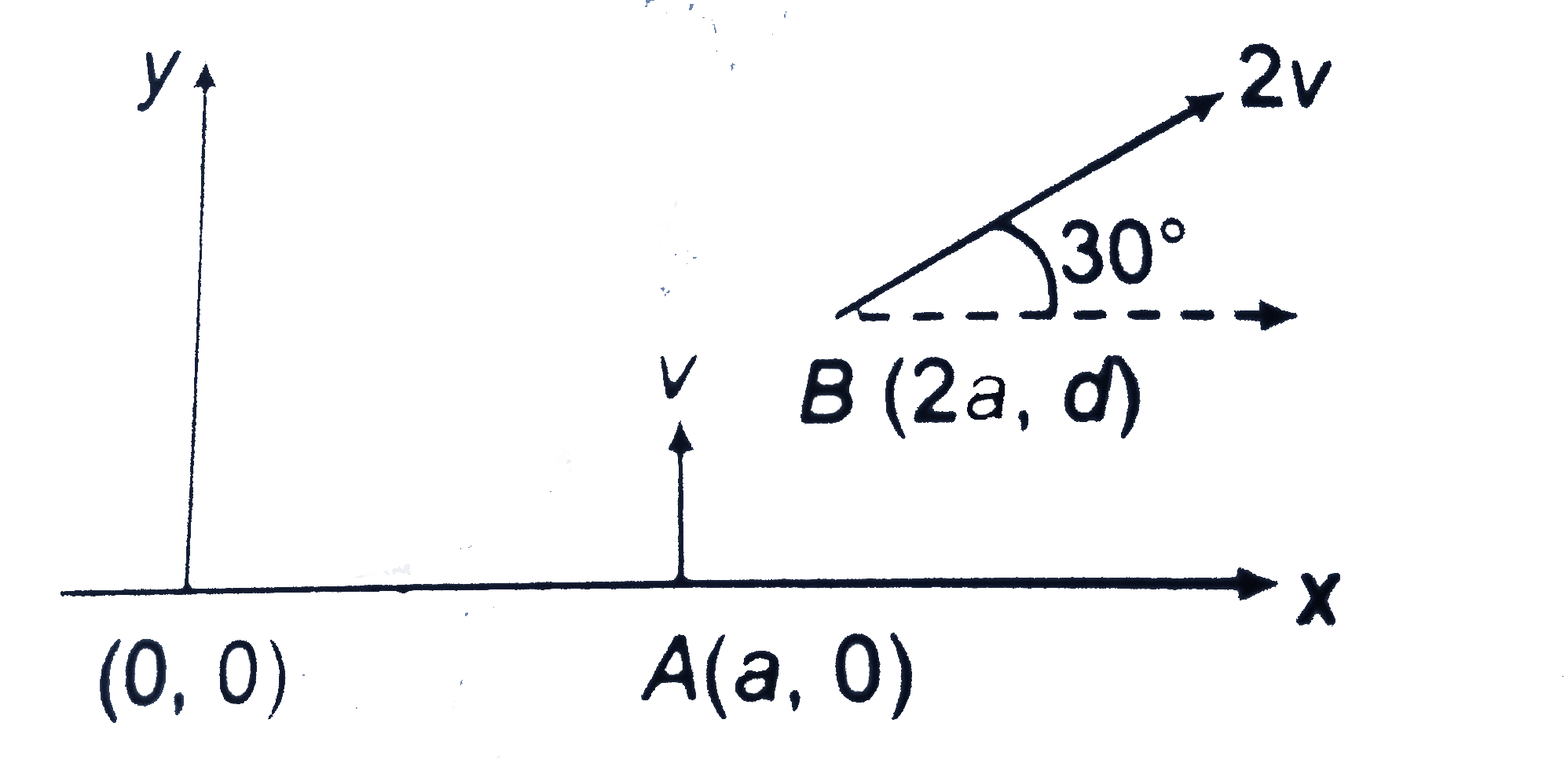
View SolutionLet V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
View SolutionA uniform field of 8 N/C exists in space in positive x-direction.
(a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z).
(b) At which points, the potential is 160 V ?
(c) It the potential at the origin is taken to be 80V, what will be the expression for the potential at a general point ?
(d) What will be the potential at the origin if the potential at x = infinity is taken to be zero ?
View SolutionLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View SolutionA uniform electric field E0 exists in a region at angle 45∘ with the x - axis. There are two point A(a,0)andB(0,b) having potential VAandVB, respectively, then
 .
.
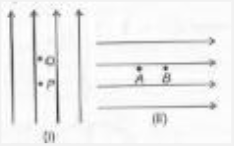
View SolutionThe uniform electric field is along positive y-axis positive x axis as shown in figure. The signs of potential differences VP−VQ and VB−VA respectively are
View SolutionA uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
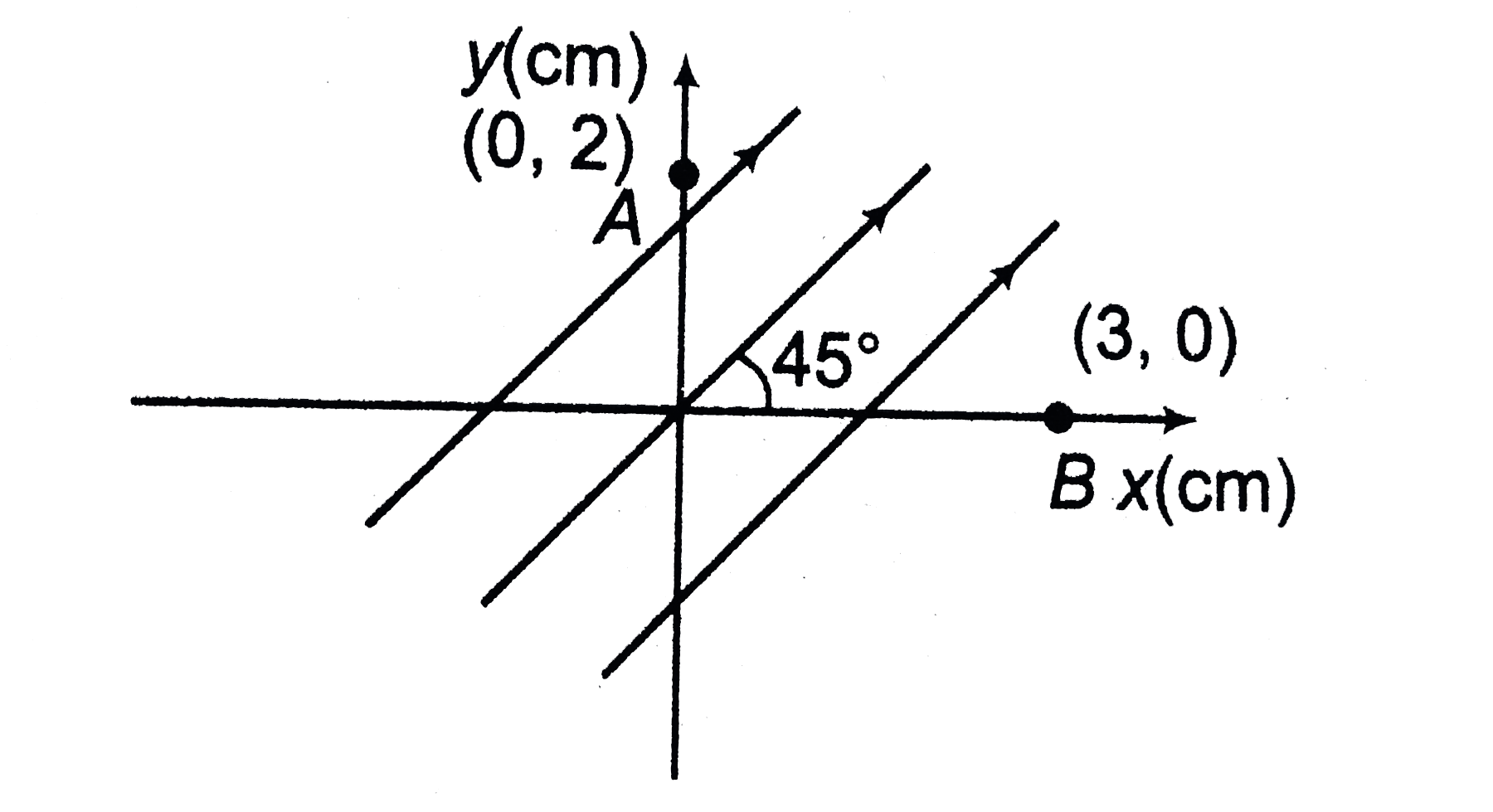
View SolutionIn the given if point C is connected to the earth and a potential of +2000 V is given to the point A, the potential at B is

View Solution
