Two rods are of same material and having same length and area. If heat ΔQ flows through them for 12 min when they are joined side by side. If now both the rods are joined in parallel, then the same amount of heat ΔQ will flow in
24 min
3 min
12 min
6 min
The correct Answer is:B
To solve the problem, we need to analyze the heat transfer through two rods connected in series and then in parallel. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Setup
We have two rods made of the same material, with the same length (L) and cross-sectional area (A). When they are connected side by side, they are in series for heat transfer.
Step 2: Heat Transfer in Series
When the rods are connected in series, the total thermal resistance (R_total) is the sum of the individual resistances:
- Let the thermal resistance of one rod be R.
- Therefore, the total resistance when in series is:
Rtotal=R+R=2R
Step 3: Heat Current Calculation in Series
The heat current (I) can be calculated using the formula:
I=ΔQT=T1−T2Rtotal
Substituting Rtotal=2R:
I=ΔQT=T1−T22R
Given that heat ΔQ flows for 12 minutes when the rods are in series, we can express this as:
ΔQ12=T1−T22R
Step 4: Heat Transfer in Parallel
Now, when the rods are connected in parallel, the equivalent thermal resistance (R_net) is given by:
1Rnet=1R+1R=2R
Thus,
Rnet=R2
Step 5: Heat Current Calculation in Parallel
The heat current in parallel can be calculated similarly:
I=ΔQT=T1−T2Rnet
Substituting Rnet=R2:
I=ΔQT=T1−T2R2=2(T1−T2)R
Step 6: Setting the Heat Currents Equal
Since the same amount of heat ΔQ flows through both configurations, we can equate the two expressions for heat current:
ΔQ12=2(T1−T2)R
Step 7: Solving for Time in Parallel
Now, we can express the time (T) for the parallel configuration:
ΔQT=2(T1−T2)R
Substituting the expression for ΔQ from the series case:
ΔQ12=2(T1−T2)R
This implies:
T12=12⟹T=12×12=6 minutes
Step 8: Conclusion
Thus, the time taken for the same amount of heat ΔQ to flow through the rods when they are connected in parallel is 6 minutes.
We have two rods made of the same material, with the same length (L) and cross-sectional area (A). When they are connected side by side, they are in series for heat transfer.
When the rods are connected in series, the total thermal resistance (R_total) is the sum of the individual resistances:
- Let the thermal resistance of one rod be R.
- Therefore, the total resistance when in series is:
Rtotal=R+R=2R
The heat current (I) can be calculated using the formula:
I=ΔQT=T1−T2Rtotal
Substituting Rtotal=2R:
I=ΔQT=T1−T22R
Given that heat ΔQ flows for 12 minutes when the rods are in series, we can express this as:
ΔQ12=T1−T22R
Now, when the rods are connected in parallel, the equivalent thermal resistance (R_net) is given by:
1Rnet=1R+1R=2R
Thus,
Rnet=R2
The heat current in parallel can be calculated similarly:
I=ΔQT=T1−T2Rnet
Substituting Rnet=R2:
I=ΔQT=T1−T2R2=2(T1−T2)R
Since the same amount of heat ΔQ flows through both configurations, we can equate the two expressions for heat current:
ΔQ12=2(T1−T2)R
Now, we can express the time (T) for the parallel configuration:
ΔQT=2(T1−T2)R
Substituting the expression for ΔQ from the series case:
ΔQ12=2(T1−T2)R
This implies:
T12=12⟹T=12×12=6 minutes
Thus, the time taken for the same amount of heat ΔQ to flow through the rods when they are connected in parallel is 6 minutes.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct
5 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Subjective
13 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
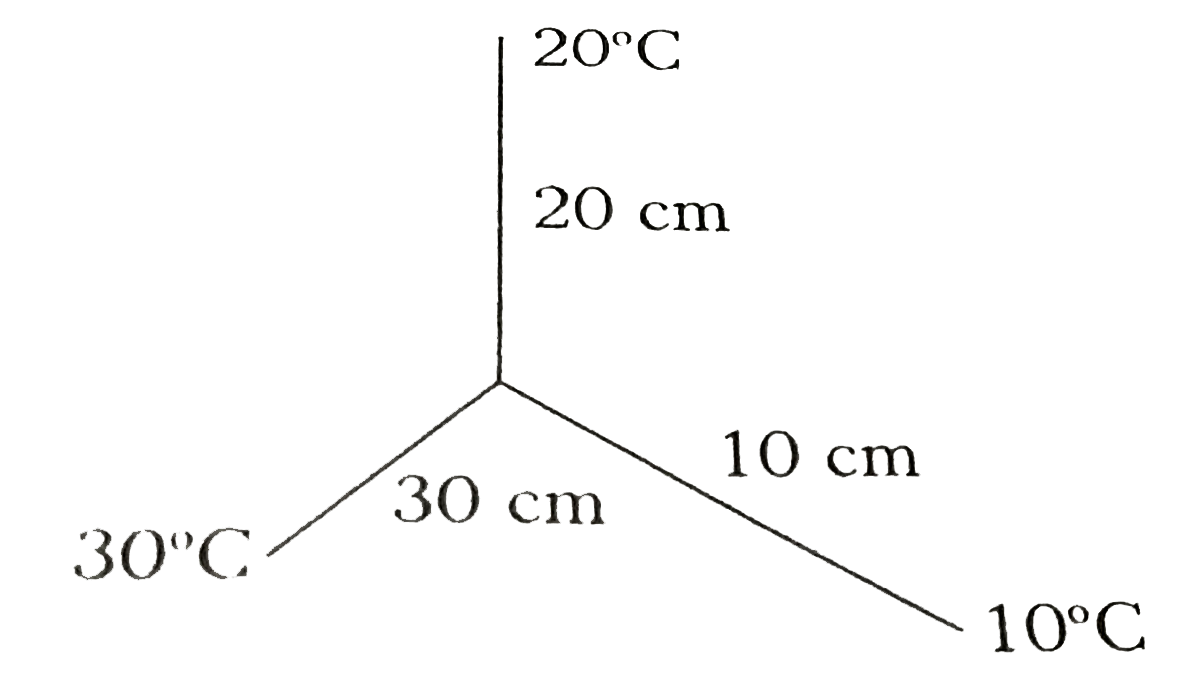
Three rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
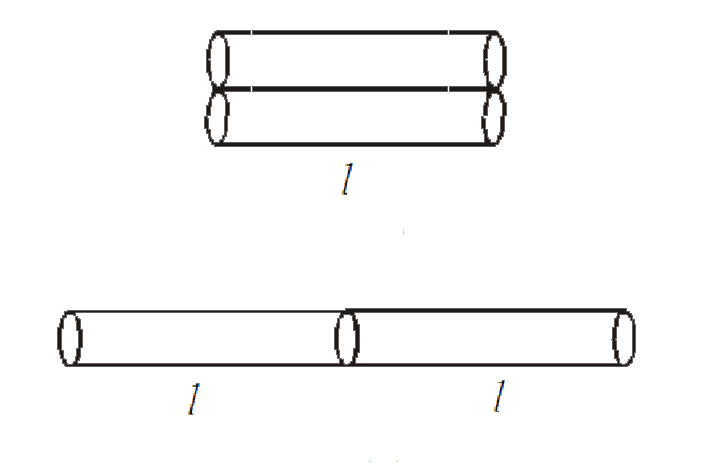
View SolutionTwo rods of same length and transfer a given amount of heat 12 second, when they are joined as shown in figure (i). But when they are joined as shwon in figure (ii), then they will transfer same heat in same conditions in
View Solution
Knowledge Check
Heat is flowing through two cylindrical rods of the same material. The diamters of the rods are in the ratio 1:2 and the length in the ratio 2:1. If the temperature difference between the ends is same then ratio of the rate of flow of heat through them will be
A1:1B1:8C2:1D8:1
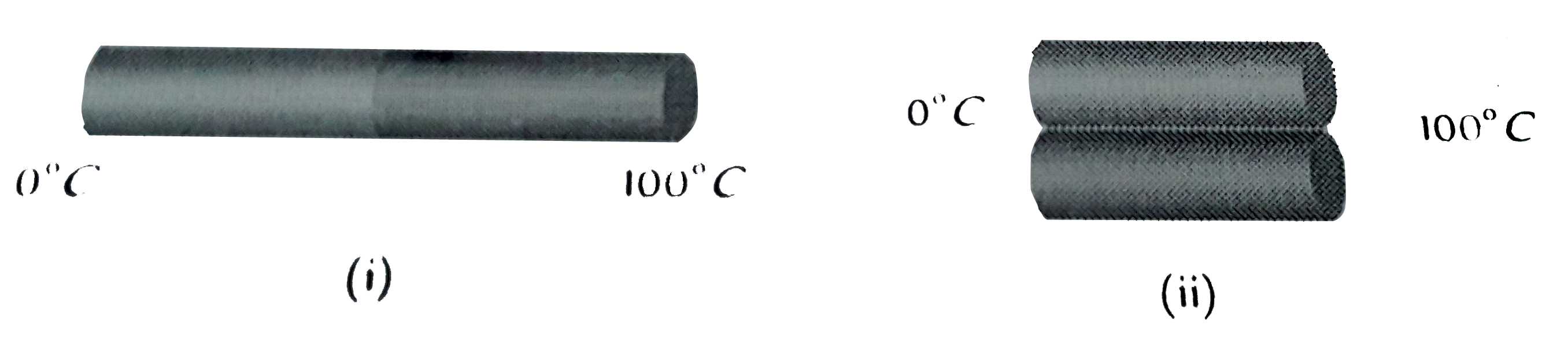
Two identical square rods of metal are welded end to end as shown in figure (i), 20 calories of heat flows through it in 4 minutes. If the rods are welded as shown in figure (ii), the same amount of heat will flow through the rods in
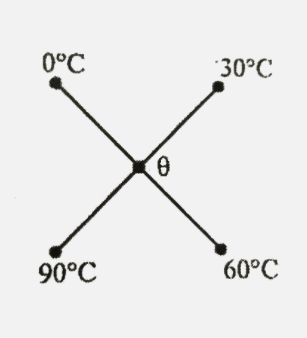
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
View SolutionTwo heater wires, made of the same material and having the same length and the same radius, are first connected in series and then in parallel to a constant potential difference. If the rate of heat produced in the two cases are Hs and Hp respectively then HsHp will be
View SolutionTwo identical metal plates are welded end to end as shown in - (i) . 20 cal of heat flows through it in 4 minutes. If the plates are welded as shown in figure-(ii) , find the time (in minutes) taken by the same amount of heat to flow through the plates.
_S01_132_Q01.png)
View SolutionHeat is flowing through two cylindrical rods of the same material . The diameters of the rods are in the ratio 1:2 and the lengths in the ratio 2:1.If the temperature difference between the ends be the same ,then the ratio of the rate of flow if heat through them will be ?
View SolutionThere are two Cu spheres having same size. One of them is hollow and the other one is solid. Which will expand more if
(i) they are heated through same temperature range.
(ii) they are supplied with same amount of heat.
View SolutionTwo balls of same material and same surface finish have their diameters in the ratio 1:2. They are heated to the same temperature and are left in a room to cool by radiation, then the initial rate of loss of heat
View Solution
