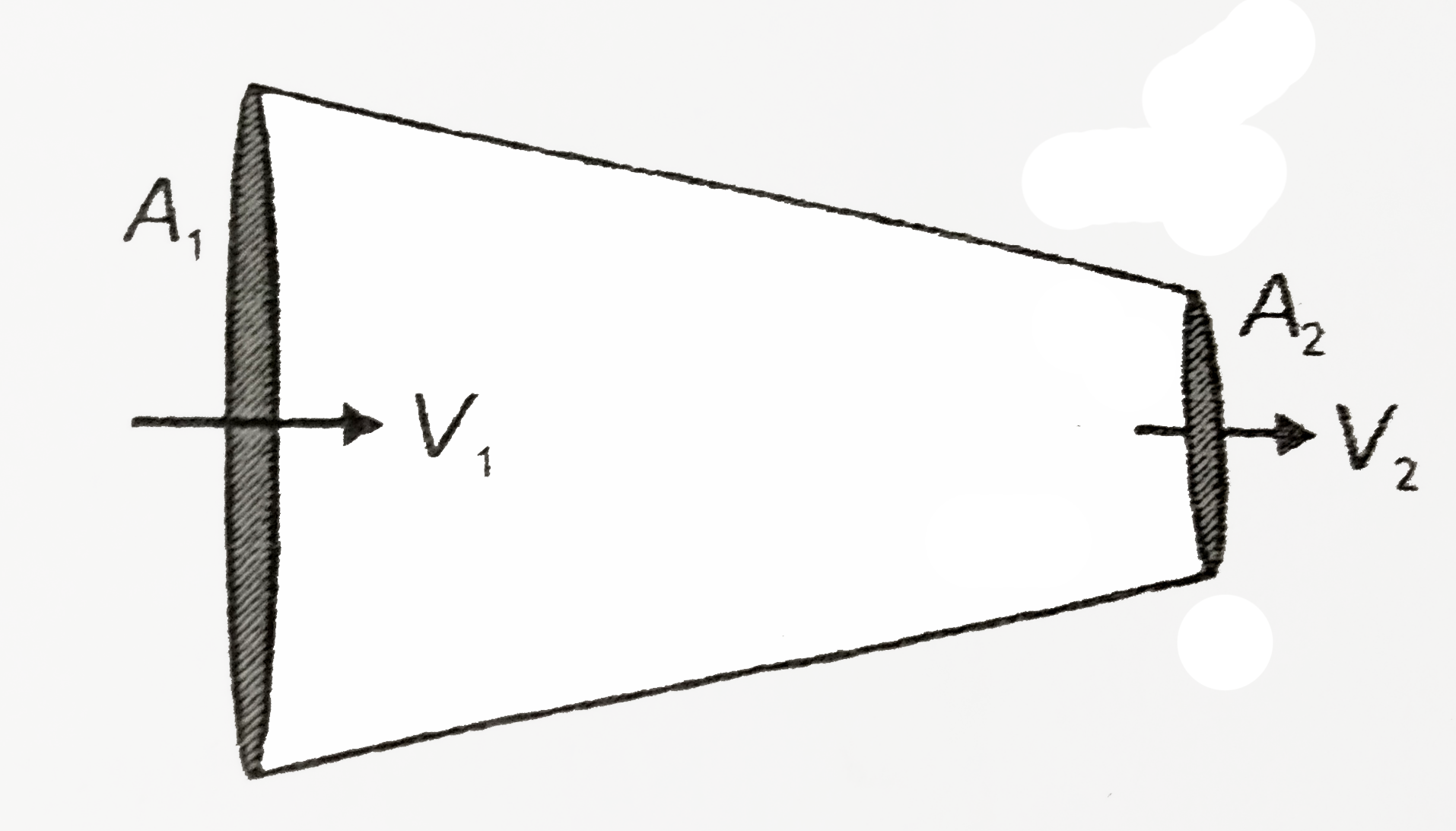
Calculate the rate of flow of glycerine of density through the conical section of a horizontal pipe, if the radii of its ends are 0.1 m and 0.04 m and the pressure drop across its length is .
The correct Answer is:A, C, D
From continuity equation,
or,
…(i)
From Bernouli's equation,

or
or ...(ii)
Solving Eqs, (i) ans (ii), we get
Rate of volume flow through the tube
.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
21 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
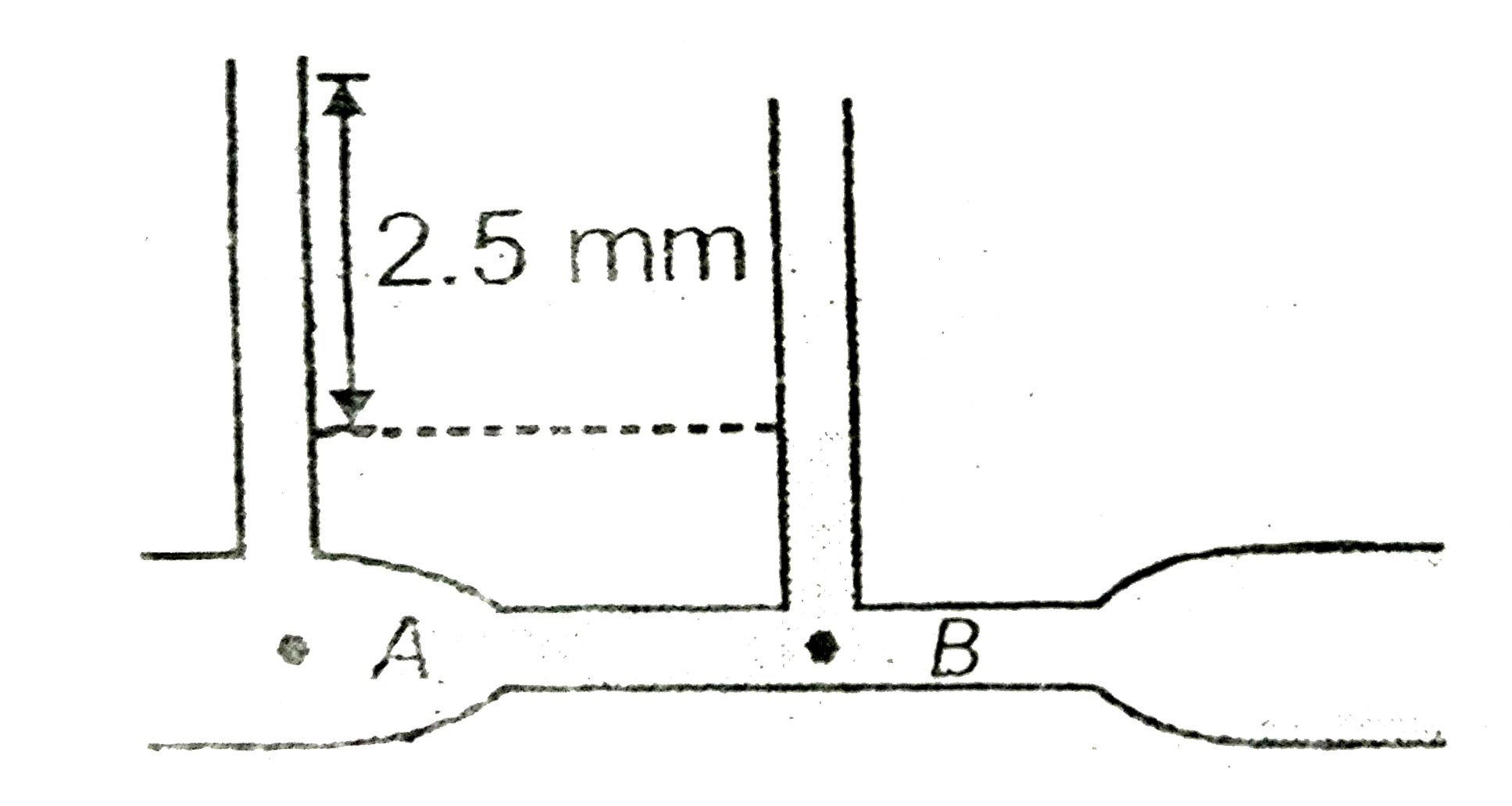
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
View SolutionThe radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
View SolutionCalculate the pH of 1.0×103 M solution of NaCI
View SolutionThe volume of a cuboid is 7.68m3 if its length = 3.2 m and height = 1.0 m find its breadth.
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View SolutionIf the ratio of principal specific heat capacities of a certain gas is 1:4 and its density at STP is 0.09 kgm−3 calculate the values of specific heat capacity at constant pressure and constant volume. [Standard atmospheric pressure =1.01×105Nm−2
View SolutionThe volume of a cuboid is 7.68m3if its length =3.2 m and height = 1.0 m : find its breadth.
View SolutionThe reading of pressure meter attached with a closed water pipe is 3.5×105Nm−2 . On opening the valve of the pipe, the reading of pressure meter is reduced to 3×105Nm−2. Calculate the speed of water flowing out of the pipe.
View Solution
