A ball with mass m is attached to the end of a rod of mass M and length l. The other end of the rod is pivoted so that the ball can move in a vartical circle. The rod is held in the horizontal position as shown in figure and then given just enough a downward push so that the ball swings down and just reaches the vertical upward position having zero speed there. Now answer the following questions.
The initial speed given to the ball is
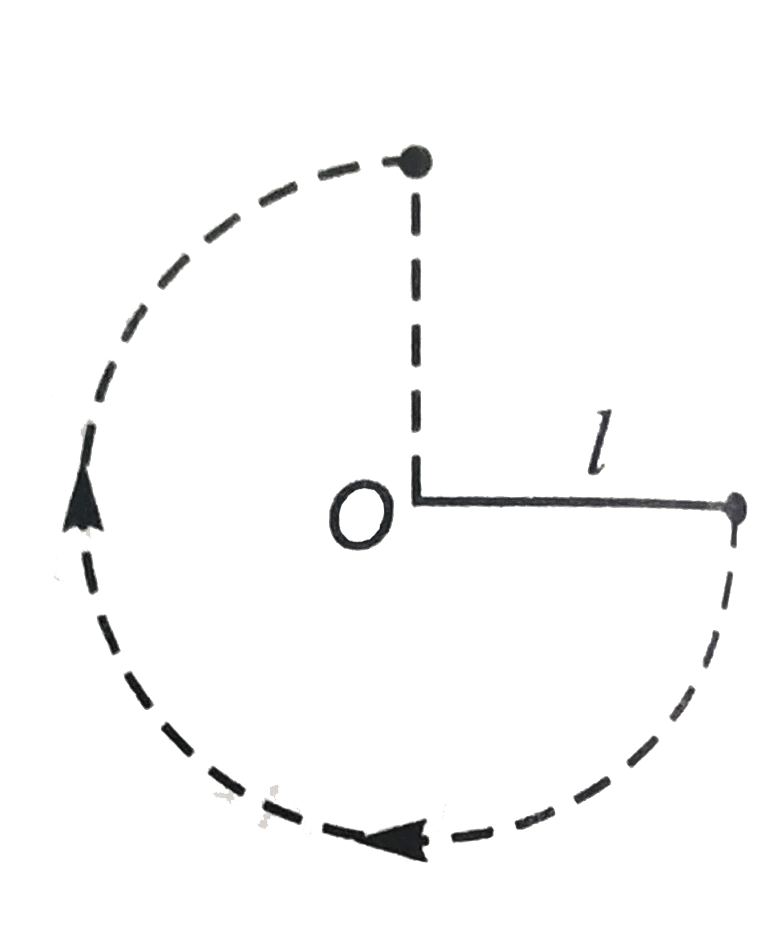
√Mgl+2mglm
√2gl
√2Mgl+mglm
None of these
The correct Answer is:D
ω=vl
Now, decrease in rotational kinetic energy = increase in potential energy
:. 12Iω3=(M2+m)gl
or 12[Ml23+ml2](vl)2=(M2+m)gl
:. v=
⎷(M2+m)gl(M6+m2)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Subjective
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
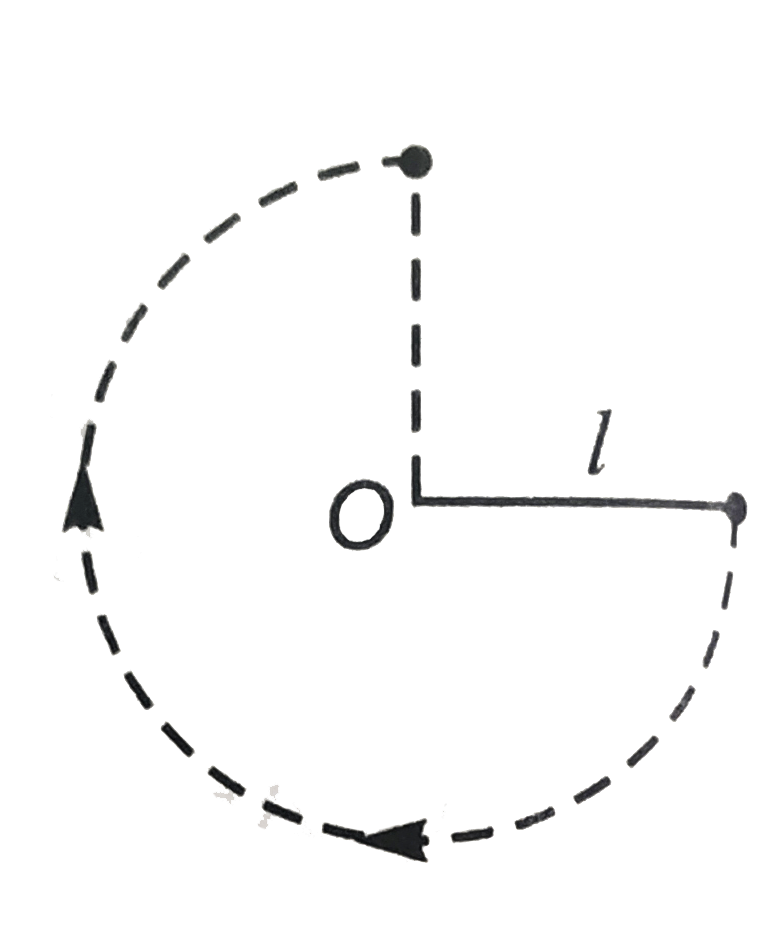
A ball with mass m is attached to the end of a rod of mass M and length l. The other end of the rod is pivoted so that the ball can move in a vartical circle. The rod is held in the horizontal position as shown in figure and then given just enough a downward push so that the ball swings down and just reaches the vertical upward position having zero speed there. Now answer the following questions.
The change in potential energy of the system (ball+rod) is
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA particle of mass m is attached to an end of a uniform rod of mass M = 2m and length l1 which is suspended through its mid point by an inextensible string as shown initially the rod is in horizontal position and at rest. The system is released from this position Just after the release
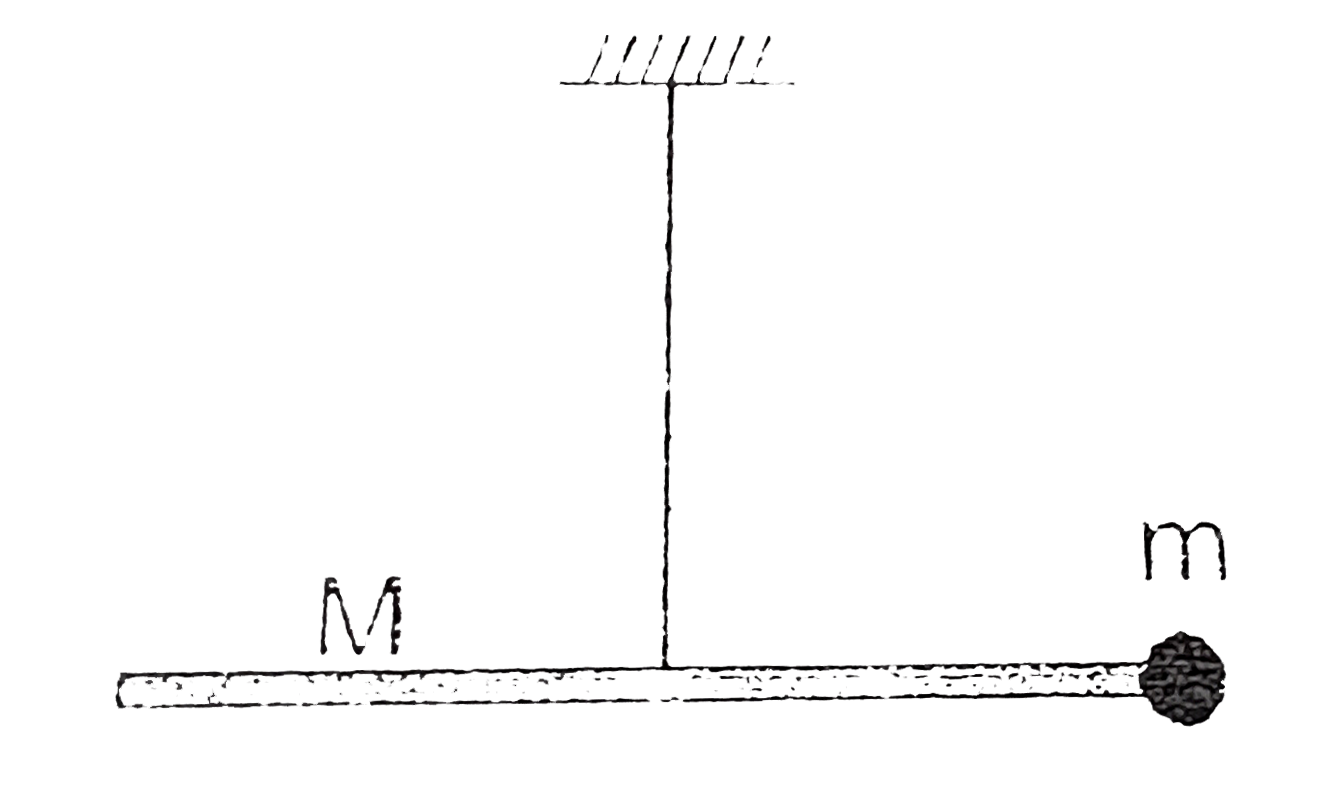
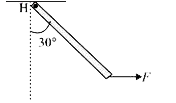
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
View SolutionTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.

View SolutionA particle of mass of mass m is attached to a light rod of lenght l other end of the rod is hinged to a wall . Minimumm velocity (Vo) that should be given to a particle in lowest positiion so that it completes a vertical circle
View SolutionA slender uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
View SolutionOne end of a light rod of length 1m is attached with a string of length 1m. Other end of the rod is attached at point O such that rod can move in a vertical circle. Other end of the string is attached with a block of mass 2kg. The minimum velocity that must be given to the block in horizontal direction so that it can complete the vertical is (g=10m/s2)
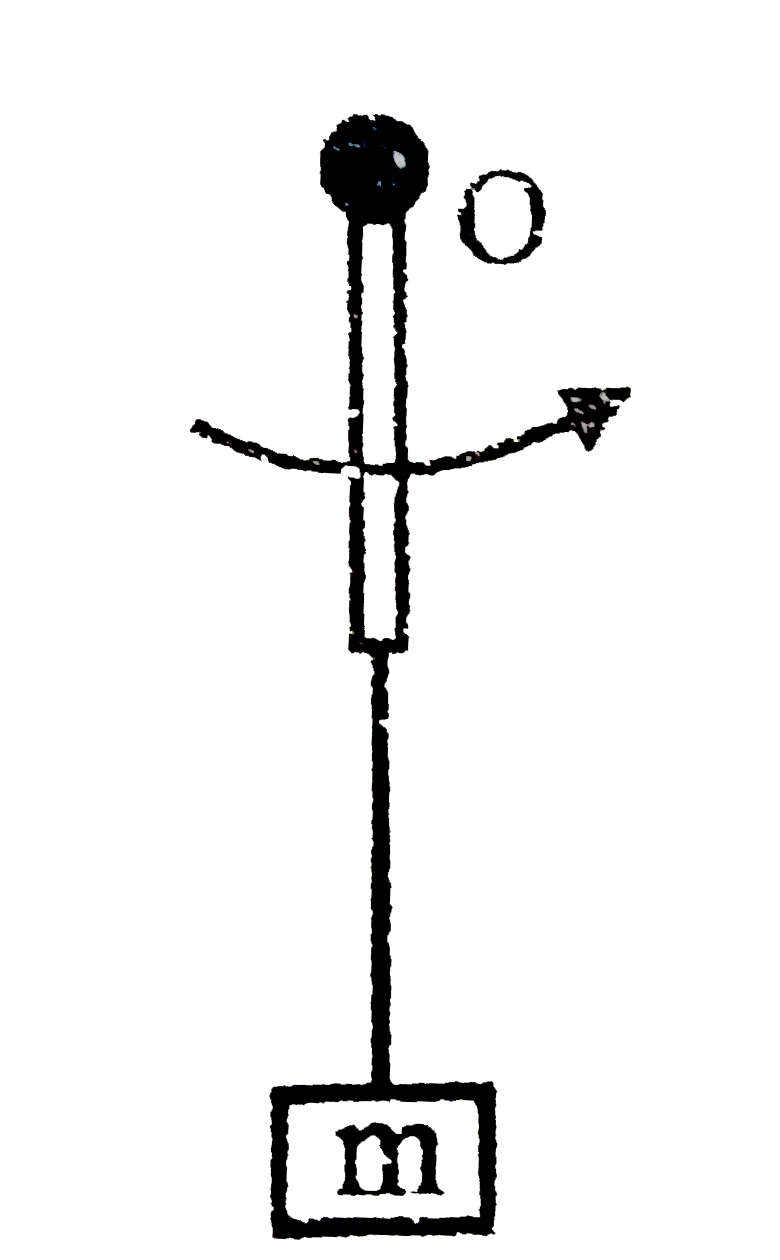
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View Solution
