Assertion : Displacement-time equation of two particles moving in a straight line are, s1=2t−4t2 and s2=−2t+4t2. Relative velocity between the two will go on increasing.
Reason : If velocity and acceleration are of same sign then speed will increase.
If the both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:D
To solve the given question, we need to analyze the displacement-time equations of the two particles and determine the relative velocity between them. Let's break this down step-by-step.
Step 1: Write down the displacement equations
The displacement equations for the two particles are given as:
- Particle 1: s1=2t−4t2
- Particle 2: s2=−2t+4t2
Step 2: Find the velocities of both particles
To find the velocities, we differentiate the displacement equations with respect to time t.
For Particle 1:
v1=ds1dt=d(2t−4t2)dt=2−8t
For Particle 2:
v2=ds2dt=d(−2t+4t2)dt=−2+8t
Step 3: Calculate the relative velocity
The relative velocity of Particle 1 with respect to Particle 2 is given by:
vrel=v1−v2
Substituting the expressions for v1 and v2:
vrel=(2−8t)−(−2+8t)=2−8t+2−8t=4−16t
Step 4: Analyze the relative velocity
Now, we need to determine if the relative velocity vrel=4−16t is increasing or decreasing over time.
- The term −16t indicates that as time t increases, the relative velocity vrel decreases because the coefficient of t is negative.
Step 5: Conclusion about the assertion
Since the relative velocity vrel is decreasing over time, the assertion that "the relative velocity between the two will go on increasing" is false.
Step 6: Analyze the reason
The reason states: "If velocity and acceleration are of the same sign, then speed will increase."
To check this, we need to consider the acceleration of both particles:
For Particle 1:
a1=dv1dt=d(2−8t)dt=−8
For Particle 2:
a2=dv2dt=d(−2+8t)dt=8
Now, we check the signs of velocity and acceleration:
- For Particle 1, at t=0, v1=2 (positive) and a1=−8 (negative) → different signs.
- For Particle 2, at t=0, v2=−2 (negative) and a2=8 (positive) → different signs.
Since the velocity and acceleration of both particles are not of the same sign, the reason is true in general, but it does not explain the assertion.
Final Answer
- Assertion: False
- Reason: True
- Therefore, the correct option is: Assertion is false, but reason is true.
The displacement equations for the two particles are given as:
- Particle 1: s1=2t−4t2
- Particle 2: s2=−2t+4t2
To find the velocities, we differentiate the displacement equations with respect to time t.
v1=ds1dt=d(2t−4t2)dt=2−8t
v2=ds2dt=d(−2t+4t2)dt=−2+8t
The relative velocity of Particle 1 with respect to Particle 2 is given by:
vrel=v1−v2
Substituting the expressions for v1 and v2:
vrel=(2−8t)−(−2+8t)=2−8t+2−8t=4−16t
Now, we need to determine if the relative velocity vrel=4−16t is increasing or decreasing over time.
Since the relative velocity vrel is decreasing over time, the assertion that "the relative velocity between the two will go on increasing" is false.
The reason states: "If velocity and acceleration are of the same sign, then speed will increase."
a1=dv1dt=d(2−8t)dt=−8
a2=dv2dt=d(−2+8t)dt=8
- For Particle 1, at t=0, v1=2 (positive) and a1=−8 (negative) → different signs.
- For Particle 2, at t=0, v2=−2 (negative) and a2=8 (positive) → different signs.
- Assertion: False
- Reason: True
- Therefore, the correct option is: Assertion is false, but reason is true.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective
50 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.9
6 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionAt time t , the displacement of a particle moving in a straight line by x=−4t2+2t . Find the velocity and acceleration a when t = (1/2) s .
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
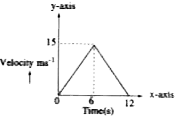
View SolutionThe velocity and time graph for a particle moving in a straight line s shown in the figure. Then, the average velocity between t=4 s and t=6 s is _____
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
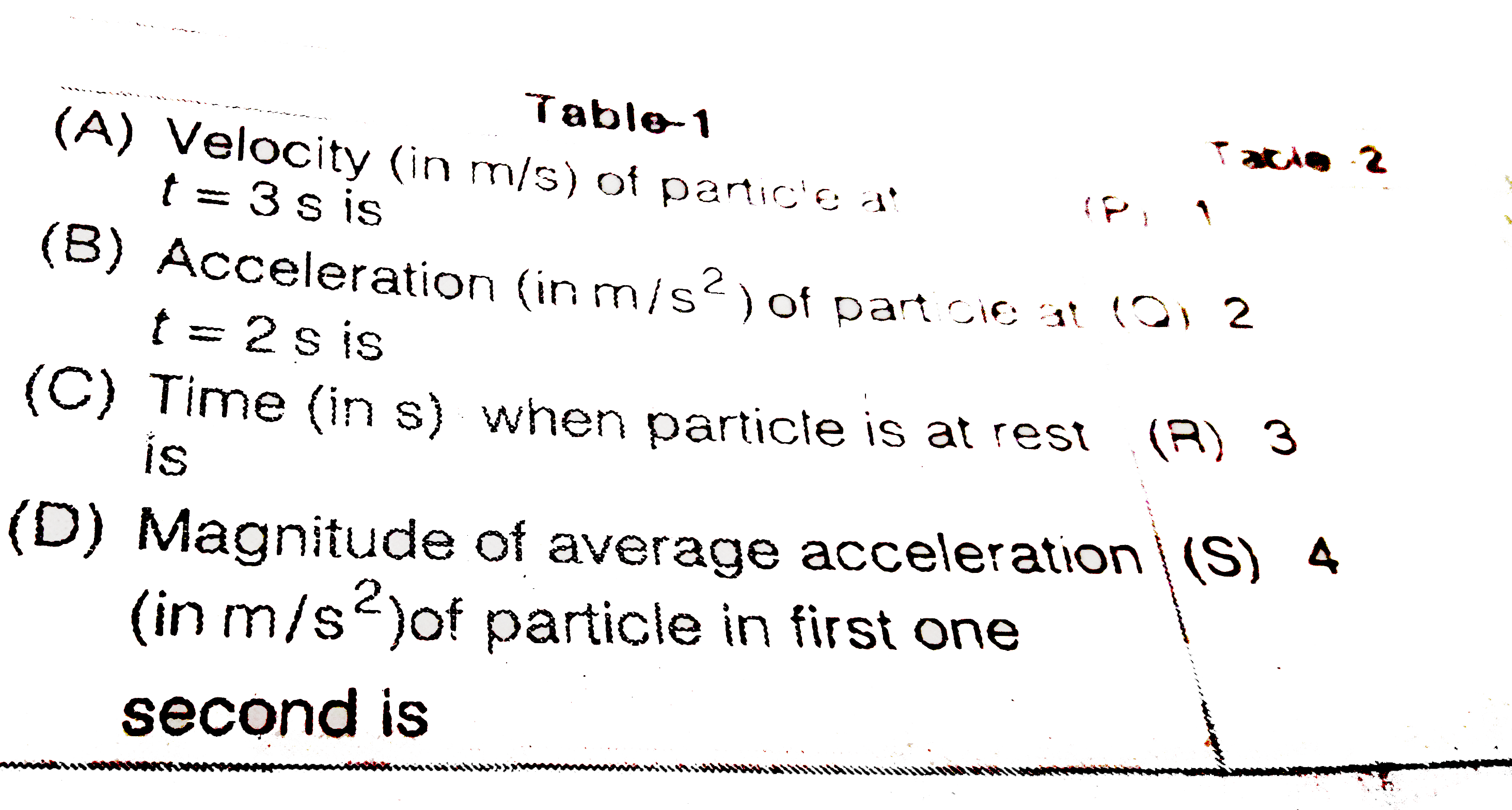
View SolutionThe velocity of a particle is zero at time t = 2s, then
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.

View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View Solution
