A cubic f(x)=ax3+bx2+cx+d vanishes at x=-2 and has relative maximum/minimum at x=- 1 and x=1/3 if ∫1−1f(x)dx=143
f(x) decreases in the intervalSolution in Telugu
(−13,1)
(−13,−1)
(−1,13)
(1,32)
The correct Answer is:C
Step by step video, text & image solution for A cubic f(x)=ax^(3)+bx^(2)+cx+d vanishes at x=-2 and has relative maximum/minimum at x=- 1 and x=1//3 if int_(-1)^(1)f(x)dx=(14)/(3) f(x) decreases in the interval by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (PRACTICE SHEET )(ADVANCED)) (INTEGER TYPE QUESTIONS)3videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (PRACTICE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)2videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III35videos
MAXIMA & MINIMA
- BOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )2videos
MEAN VALUE THEOREMS
Similar Questions
Number of integral values of b for which the equation x33−x=b has three distinct solution is ____
03:34View SolutionMatch the following Column I to Column II
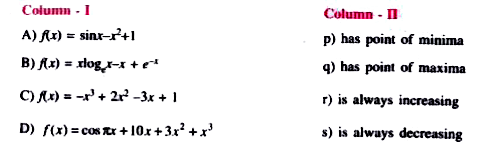
06:52View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
03:34View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )02:56View SolutionA cubic function f(x) vanishes at x=−2 and has relative minimum/maximum at x=−1andx=13if∫1−1f(x)dx=143. Find the cubic function f(x).
04:46View SolutionA cubic polynomial y=f(x) has a relative minimum at x=1& maximum at x=-2. If f(0)=1 then
04:24View SolutionIf f(x)=x^(3)+ax^(2)+bx+c is minimum at x=3 and maximum at x=-1, then
View SolutionIf f(x)=x^(3)+ax^(2)+bx+c is minimum at x=3 and maximum at x=-1, then-
08:18View SolutionLet f(x)=x3+ax2+bx+c, where a, b, c are real numbers. If f(x) has a local minimum at x=1 and a local maximum at x=−13 and f(2)=0, then ∫1−1f(x)dx equals-
08:07View SolutionA cubic function f(x) tends to zero at x=-2 and has relative maximum/ minimum at x=-1 and x=13. If ∫1−1f(x)dx=143. Find the cubic function f(x).
08:14View SolutionSuppose a, b, c,d be non-zero real number and ab>0, and ∫10(1+ex2)(ax3+bx2+cx+d)dx=∫20(1+ex2)
(ax3+bx2+cx+d)dx=0
If f(x)=∫f(x)dx=∫10f(x)dx=∫20f(x)dx=0
then in which of the following can Rolle's theorem can be applied for F(x), where
f(x)=(1+ex2)(ax3+bx2+cx+d)09:40View SolutionA cubic function f(x) vanishes at x=−2 and has relative maximum/minimum at x=−1 and x=13. If ∫1−1f(x)dx=143, find the cubic function f(x).
10:53View SolutionIf f(x)=ax3+bx2+cx have relative extrema x = 1 and at x = 5. If ∫1−1f(x)dx=6 then :
11:32View Solutionएक तीन घातीय बहुपद f(x),x=−2 पर शून्य हो जाता है तथा उसके x=−1 एवं x=1/3 पर सापेक्षित उच्चिष्ठ एवं निम्निष्ठ है यदि ∫1−1f(x)dx=143 हो, तो f(x) ज्ञात कीजिये।
View Solutionएक घनीय बहुपद f(x), x =-2 पर लुप्त होता है तथा इसका सापक्षिक निम्निष्ठ/उच्चिष्ठ x =-1 तथा x = 1/3 पर है। यदि 1∫−1f(x)dx=143 तो (f(x)) ज्ञात कीजिए |
11:29View SolutionCubic equation f(X) = ax^3 + bx^2 + cx + d, x =-2 But is equal to zero and the spatial high / low value x = -1 and x= 1/3 Is on and if int_(-1)^(1) f(x) dx =(14)/(3) C The value of
10:19View Solution