Computer is generating binary digits , Probability of '0' at odd position is 13 and probability of '0' at even position is 12 . Find the probability that 10 is immediately followed by 01
The correct Answer is:19
To solve the problem of finding the probability that the sequence "10" is immediately followed by "01" in a binary digit generation scenario, we can break it down step-by-step.
Step 1: Understand the Problem
We need to find the probability of the sequence "1001" occurring in the binary digits generated by the computer. The probabilities of generating '0' and '1' at odd and even positions are given as follows:
- Probability of '0' at odd positions = 13
- Probability of '1' at odd positions = 1−13=23
- Probability of '0' at even positions = 12
- Probability of '1' at even positions = 1−12=12
Step 2: Identify the Positions
In the sequence "1001":
- The first '1' is at position 1 (odd)
- The first '0' is at position 2 (even)
- The second '0' is at position 3 (odd)
- The second '1' is at position 4 (even)
Step 3: Calculate the Probability for Each Position
Now we calculate the probability for each digit in the sequence "1001":
1. Probability of '1' at position 1 (odd) = 23
2. Probability of '0' at position 2 (even) = 12
3. Probability of '0' at position 3 (odd) = 13
4. Probability of '1' at position 4 (even) = 12
Step 4: Multiply the Probabilities
Now, we multiply the probabilities of each digit in the sequence "1001":
P(1001)=P(1 at position 1)×P(0 at position 2)×P(0 at position 3)×P(1 at position 4)
=(23)×(12)×(13)×(12)
Step 5: Perform the Multiplication
Calculating the above expression:
=23×12×13×12=2×1×1×13×2×3×2=236=118
Step 6: Final Result
Thus, the probability that the sequence "10" is immediately followed by "01" is:
118
We need to find the probability of the sequence "1001" occurring in the binary digits generated by the computer. The probabilities of generating '0' and '1' at odd and even positions are given as follows:
- Probability of '0' at odd positions = 13
- Probability of '1' at odd positions = 1−13=23
- Probability of '0' at even positions = 12
- Probability of '1' at even positions = 1−12=12
In the sequence "1001":
- The first '1' is at position 1 (odd)
- The first '0' is at position 2 (even)
- The second '0' is at position 3 (odd)
- The second '1' is at position 4 (even)
Now we calculate the probability for each digit in the sequence "1001":
1. Probability of '1' at position 1 (odd) = 23
2. Probability of '0' at position 2 (even) = 12
3. Probability of '0' at position 3 (odd) = 13
4. Probability of '1' at position 4 (even) = 12
Now, we multiply the probabilities of each digit in the sequence "1001":
P(1001)=P(1 at position 1)×P(0 at position 2)×P(0 at position 3)×P(1 at position 4)
=(23)×(12)×(13)×(12)
Calculating the above expression:
=23×12×13×12=2×1×1×13×2×3×2=236=118
Thus, the probability that the sequence "10" is immediately followed by "01" is:
118
Similar Questions
The probability of events E1 and £2 occurs is 0.6 and 0.4. Find the probability of E1 & E2 .
View SolutionThe probability of A winning a race is 1/2, and that for B is 1/3. Find the probability that
both win
View SolutionThe probability of A winning a race is 1/2, and that for B is 1/3. Find the probability that
only B wins
View SolutionThe probability of A winning a race is 1/2, and that for B is 1/3. Find the probability that
only A wins
View SolutionLet a computer program generate only the digits 0 and 1 to form a string of binary numbers with probability of occurrence of 0 at even places be 12 and probability of occurrence of 0 at the odd place be 13. Then the probability that '10' is followed by '01' is equal to :
View SolutionThe probability of A winning a race is 1/2, and that for B is 1/3. Find the probability that
none of them wins
View SolutionOdds in favour of an event is 2:3. Find the probability of happening of an event.
View SolutionThe following probability distribution of r.v. X
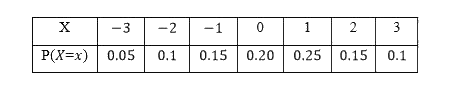
Find the probability that (i) X is positive. (ii) X is odd
View SolutionThe probability of A winning a race is 1/2, and that for B is 1/3. Find the probability that
only one of them wins
View SolutionThere are 5 independent trials , probability of exactly one success is 0.4096 , probability of exactly 2 success is 0.2048. Find probability of exactly 3 success
View Solution
