θ=30∘ के लिए निम्नलिखित में से प्रत्येक को सत्यापित कीजिए।
cos2θ=2cos2θ−1=1−2sin2θ
The correct Answer is::cos2θ=2cos2θ−1=1−2sin2θ
Step by step video, text & image solution for theta=30^(@) के लिए निम्नलिखित में से प्रत्येक को सत्यापित कीजिए। cos2theta=2cos^(2)theta-1=1-2sin^(2)theta by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय BOOK - S CHANDCHAPTER - त्रिकोणमितीय EXERCISE - प्रश्नावली 27.1
30 Videos
- त्रिकोणमितीय BOOK - S CHANDCHAPTER - त्रिकोणमितीय EXERCISE - प्रश्नावली 27.2
31 Videos
- त्रिकोणमितीय BOOK - S CHANDCHAPTER - त्रिकोणमितीय EXERCISE - प्रश्नावली 27.3
11 Videos
- ज्यामितीय रचनाएँBOOK - S CHANDCHAPTER - ज्यामितीय रचनाएँEXERCISE - प्रश्नावली 26.2
14 Videos
- त्रिभुज BOOK - S CHANDCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 18.2 रिक्त स्थानों को भरे :
5 Videos
Similar Questions
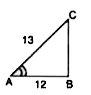
आकृति से sinA,cosA,tanA,cosecA,secA तथा cotA के मान ज्ञात कीजिए।
View Solutionनिम्नलिखित में से प्रत्येक के मान ज्ञात कीजिए :
sin60∘cos30∘+cos60∘sin30∘
View Solutionत्रिभुज ABC में कोण B समकोण है। त्रिभुज के शेष अवयव ज्ञात कीजिए यदि :
∠C=45∘,AB=5 सेमी
View Solutionएक त्रिभुज के आधार की लंबाई 5cm दो शेष भुजाओं की लंबाई का योग 7.8cm है तथा इसका आधार कोण 60∘ है, तो परिमाप होगा।
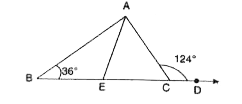
View Solutionयदि ∠ACD=124∘,∠ABC=36∘, तो ∠BAC=………….
View SolutionIf cotθ=158, then Evaluate (2+2sinθ)(1−sinθ)(1+cosθ)(2−2cosθ)
View Solution17*cos^(4)theta-sin^(4)theta is equal to (a)1-2sin^(2)((theta)/(2))(b)2cos^(2)theta-1(c)1+2sin^(2)((theta)/(2))(d)1+2cos^(2)theta
View SolutionIf 2cos^(2)theta-2sin^(2)theta=1, then theta is equal to
View Solution2(cos theta+cos2 theta)+(1+2cos theta)sin2 theta=2sin theta
View SolutionIf 2cos^(2)theta-2sin^(2)theta=1, then theta equals to
View SolutionGiven that sin theta+2cos theta=1 then prove that 2sin theta-cos theta=2
View SolutionThe vertices of a triangle are (1,sqrt(3)),(2cos theta,2sin theta) and (2sin theta,-2cos theta) where theta in R. The locus of orthocentre of the triangle is
View SolutionThe vertices of a triangle are (1,sqrt(3)),(2cos theta,2sin theta) and (2sin theta,-2cos theta) where theta in R. The locus of orthocentre of the triangle is
View SolutionThe vertices of a triangle are (1,sqrt(3)),(2cos theta,2sin theta) and (2sin theta,-2cos theta) where theta in R. The locus of orthocentre of the triangle is
View Solutionsec^(2)theta-(sin^(2)theta-2sin^(4)theta)/(2cos^(4)theta-cos^(2)theta)=1
View SolutionTaking θ=30∘, verify each of the following
(i)sin2θ=2sinθcosθ
(ii)cosθ=2cos2θ−1=1−2sin2θ
(iii)tan2θ=2tanθ1−tan2θ
View Solution
