A mathematical representation is given below:
ΔX×Δpx≥h4π
a) Which principle is illustrated by this equation?Solution in Malayalam
Step by step video & image solution for A mathematical representation is given below: DeltaX xx Deltap_(x) ge h/(4pi) a) Which principle is illustrated by this equation? by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Calculate the number of electrons which will together weigh one gram.
View SolutionWhat will be the minimum pressure required to compress 500 dm3 of air at 1 Bar to 200 dm3 at 30°C ?
View SolutionThe aqueous solution of borax is
View SolutionThe mass m of an electron is 9.1×1031kg and the velocity v of an electron in the first Bohr orbit of a hydrogen atom is 2.2×106ms−1. Assuming that the velocity is known within 10%(Δv=0.22×106ms−1), calculate the uncertainty in the electron's position in a hydrogen atom.
Strategy: According to Heisenberg's principle, the uncertainty in the postion (Δx) of any moving particle multiplied by the uncertainity of momentum (Δpx) can never be less than h/4π. In the given case, Δv is known and we need to find Δx.
View SolutionIn mathematical terms, Heisenberg's principle states that the uncertainty in the electron's position, Deltax , times the uncertainty in its momentum, Deltapx , is_____the quantity h//4pi . (i) equal to (ii) less than (iii) greater than
View SolutionThe uncertainty in the position of an electron (mass=9.1×10−28g) moving with a velocity of 3.0×104cms−1 accurate up to 0.001% will be
(Use h4π in the uncertainty expression, where h=6.626×10−27erg−s)
View SolutionA german physicist gae a principle about the uncertainties in simultaneous measurement of position and momentum of small particles. According to that physicist. It is impossible to measure simultaneously the position and momentum of small particle with absolute accuracy or certainty. if an attempt is made to measure any one of these two quantities with higher accuracy, the other becomes less accurate. The produce of the uncertainty in position (Deltax) and uncertainty momentum (Delta p) is always constant and is equal to or greater than h//4pi , where h is Planck's constant i.e. (Deltax ) (Deltap) ge (h)/(4pi) If uncertainty in momentum is twice the uncertainty in position of an electron then uncertainty in velocity is: [bar(h)=(h)/(2pi)]
View SolutionWhich of the following equation is best representation of given graph's?
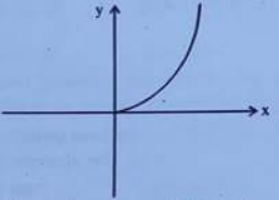
View SolutionWhich of the following equation is best representation of given graph's?
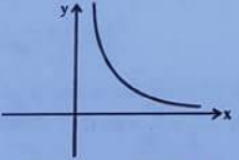
View SolutionWhich of the following equation is best representation of given graph's?

View SolutionWhich of the following equation is best representation of given graph's?
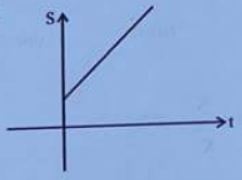
View SolutionBy the principle of mathematical induction , prove that for n≥1
View SolutionState heisenberg's uncertainty principle. Write the mathematical equation.
View SolutionUsing first principles, find the derivative of the function
y=−cotx−x.
We find Δy=−cot(x+Δx)−(x−Δx)+cotx+x
=cotx−cot(x+Δx)
View SolutionThe given below diagram is the representation of

View Solution
