व्यंजक tanA1−cotA+cotA1−tanA को लिखा जा सकता है
sec A cosec A + 1
tan A + cot A
sec A + cosec A
sin A cos A + 1
The correct Answer is:A
Step by step video, text & image solution for व्यंजक (tan A)/(1-cot A) + (cot A)/(1-tan A) को लिखा जा सकता है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE - 4 (POTENTIAL PROBLEMS BASED ON CBSE)
15 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE - 5 (RANK BOOSTER)
10 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE -3 SECTION-A (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS)
9 Videos
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-5 (RANK BOOSTER)
13 Videos
- CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)BOOK - BANSAL HINDICHAPTER - CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)EXERCISE - EXERCISE - 5
18 Videos
Similar Questions
यदि दो वृत्तों के समान लम्बाई वाले चाप केन्द्रो पर क्रमशः 60∘ तथा 75∘ के कोण बनाते हो तो उनकी त्रिज्याओं का अनुपात ज्ञात कीजिए ।
View Solutionमाना cosπ7+cos2π7−2 cos3π7 का यथार्थ मान एक परिमेय संख्या है जो कि pq के रूप में है, जहाँ p तथा q पूर्णांक है | (p + q) का मान ज्ञात कीजिए |
View Solutionइकाई त्रिज्या के तीन सिक्के (coins) एक समबाहु त्रिभुज में इस प्रकार से रखे जाते है कि वे परस्पर एक दूसरे को तथा त्रिभुज की भुजाओं को स्पर्श करते है तो त्रिभुज का क्षेत्रफल होगा
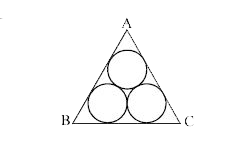
View Solutionदर्शाइये की गुणनफल, [1+(1+i2)][1+(1+i2)2][1+(1+i2)22].......[1+(1+i2)2n] का मान (1−122n)(1+i) के बराबर है, जहाँ n≥2 है।
View Solutionबिन्दु P(h, k) से परवलय x2=8y पर तीन अभिलम्ब डाले गये है तथा m1,m2 तथा m3 इन तीनों की प्रवणताऐं है। इन तीनों अभिलम्बों की प्रवणताओं का बीजगणितीय योग ज्ञात कीजिए।
View SolutionProve that (tan phi)/(1-cot phi)+(cot phi)/(1-tan phi)=1+tan phi+cot phi
View SolutionLet α=som−1(3685),β=cos−1(45)andγ=tan−1(815) then cotα+cotβ+cotγ=cotαcotβcotγ tanαtanβ+tanβtanγ+tanαtanγ=1 tanα+tanβ+tanγ=tanαtanβtanγ cotαcotβ+cotβcotγ+cotαcotγ=1
View SolutionProve the following identities: tanA1−cotA+cotA1−tanA=1+tanA+cotA=1+secAcosecA
View Solution(tan A) / (1-cot A) + (cot A) / (1-tan A) = 1 + tan A + cot A = 1 + sec A cos ecA
View SolutionFind
tanA(1−cotA)+cotA(1−tanA)
View Solutioncot(tan−1a+cot−1a)
View SolutionThe expression (tan A)/(1- cot A) + ( cot A )/( 1- tan A) can be written as
View SolutiontanA+tanBcotA+cotB+1−tanAtanB1−cotAcotB=
View Solutiontan(cot−1a)=cot(tan−1a)
View SolutionThe Expression (Tan A)/(1- cot A) +(cot A)/(1- Tan A) can be written as
View Solution1tan3A−tanA−1cot3A−cotA= .............. A) tanA B) tan2A C) cotA D) cot2A
View Solution
