A tangential force F is applied on a disc of radius R, due to which it deflects through an angle from its initial position. The work done by this force would be
FR
The correct Answer is:D
To solve the problem of calculating the work done by a tangential force F applied to a disc of radius R that deflects through an angle θ, we can follow these steps:
1. Understanding the Setup:
- We have a disc of radius R that is initially at rest.
- A tangential force F is applied at the edge of the disc, causing it to rotate about its center.
2. Identifying the Torque:
- The torque τ generated by the tangential force F can be calculated using the formula:
τ=R×F
- Here, R is the radius of the disc, and F is the tangential force applied.
3. Relating Torque to Angular Displacement:
- The work done W in rotational motion can be expressed in terms of torque and angular displacement:
W=τ×θ
- Where θ is the angular displacement in radians.
4. Substituting Torque into the Work Done Formula:
- Now, substituting the expression for torque into the work done formula:
W=(R×F)×θ
- This simplifies to:
W=F×R×θ
5. Final Expression for Work Done:
- Therefore, the work done by the tangential force F when the disc deflects through an angle θ is:
W=FRθ
Conclusion:
The work done by the tangential force F on the disc is given by the formula:
W=FRθ
- We have a disc of radius R that is initially at rest.
- A tangential force F is applied at the edge of the disc, causing it to rotate about its center.
- The torque τ generated by the tangential force F can be calculated using the formula:
τ=R×F
- Here, R is the radius of the disc, and F is the tangential force applied.
- The work done W in rotational motion can be expressed in terms of torque and angular displacement:
W=τ×θ
- Where θ is the angular displacement in radians.
- Now, substituting the expression for torque into the work done formula:
W=(R×F)×θ
- This simplifies to:
W=F×R×θ
- Therefore, the work done by the tangential force F when the disc deflects through an angle θ is:
W=FRθ
The work done by the tangential force F on the disc is given by the formula:
W=FRθ
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on rolling on incline plane)
28 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View Solution
A ball of mass 200g is attached to a string of length 50cm and a force F is applied on it as shown. Find the work done by this force if string makes an angle 60∘ with vertical. In the initial and final position, speed of the ball is zero.
View Solution
Knowledge Check
If a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
AgrBg/rC2grD2grAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
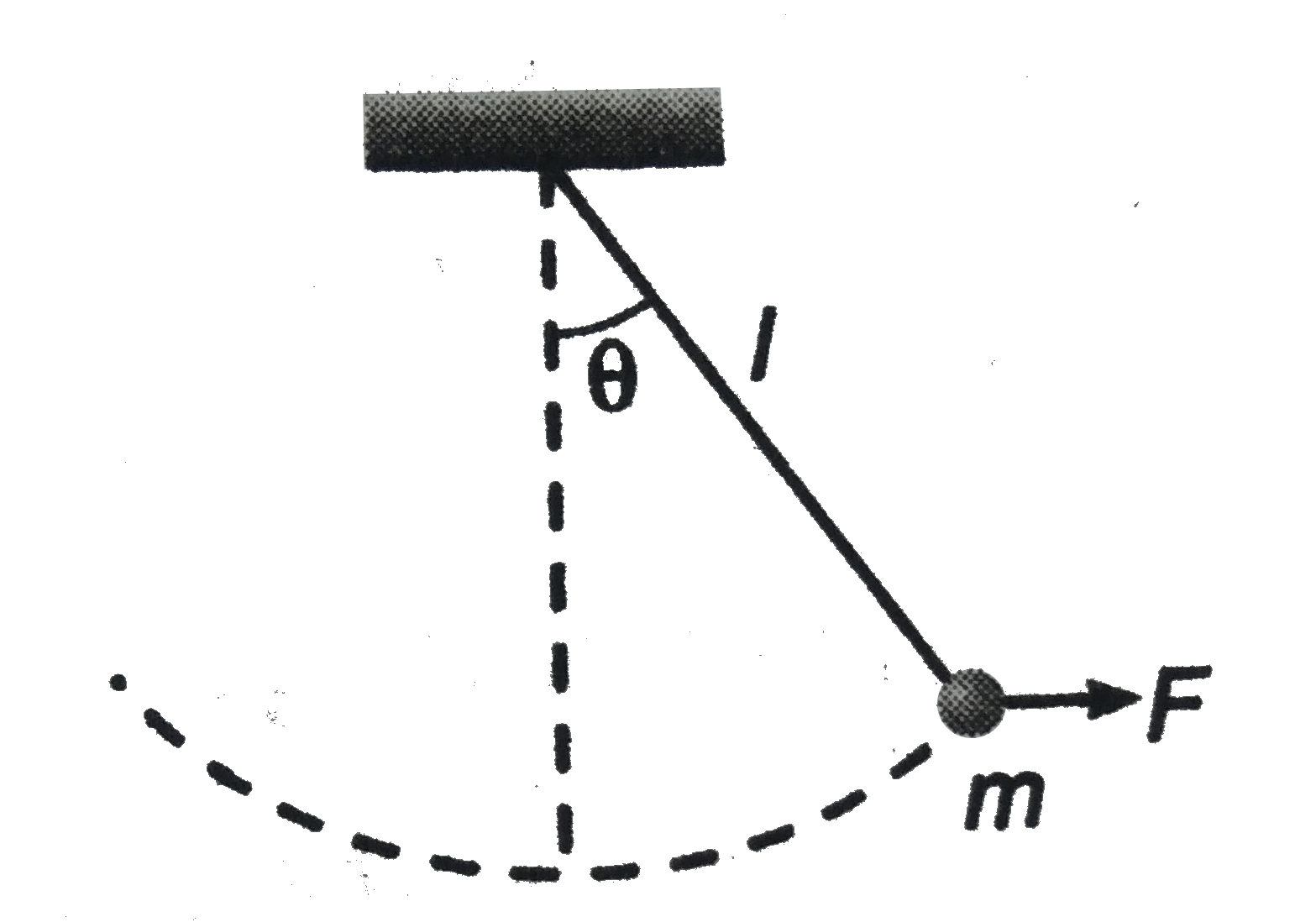 . Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)
. Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)A force F is applied on a lawn move at an angle of 60∘ with the horizontal. If it moves through a distance x, the work done by the force is
AFx/2BF/2xC2FxD2x/F
Find the work done if a force of 2000 N is applied on a load and the load moves through a distance of 100 cm .
View SolutionFind the work done if a force of 2000 N is applied on a load and the load moves through a distance of 100 cm .
View SolutionA force of 20 N acts on a body and the body moves through 1 m at an angle of45∘ in the direction of the force. The work done by the force is
View SolutionA force F=(xˆi+2yˆj)N is applied on an object of mass 10 kg, Force displaces the object from position A(1, 0) m to position B(3, 3) m then the work done by the force is (x and y are meter)
View SolutionA body, acted upon by a force off 50N is displaced through a distance 10 meter in a direction making and angle to 60∘ with the force. The work done by the force be
View Solution
