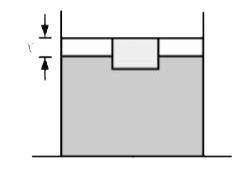
A solid cube floats in a liquid of density $ρ$ with half of its volume submerged as shown. The side length of the cube is a, which is very small compared to the size of the container. Now a liquid of density $\frac{ρ}{3}$ (immiscible with the liquid already in the container) is poured slowly into the container. The column of the liquid of density $\frac{ρ}{3}$ that must be poured so that the cube is fully submerged (with its top surface coincident with the surface of the poured liquid) is :

$\frac{a}{3}$

$\frac{a}{2}$

$\frac{2 a}{3}$

$\frac{3 a}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

A block of density $ρ$ floats in a liquid with its one third volume immersed. The density of the liquid is
A $ρ$
B $\frac{ρ}{3}$
C $\frac{ρ}{2}$
D $3 ρ$
A solid of density D is floating in a liquid of density d. If v is the volume of solid submerged in the liquid and V is the total volume of the solid, then (v)/(V) is equal to
A $\frac{d}{V}$
B $\frac{D}{d}$
C $\frac{D}{(D + d)}$
D $\frac{D + d}{D}$
A solid of density D is floating in a liquid of density d. If V is the volume of solid submerged in the liquid and V is the total volume of the solid, then $V / V$ is equal to
A $\frac{d}{D}$
B $\frac{D}{d}$
C $\frac{D}{d + D}$
D $\frac{D + d}{D}$