I : Every strictlyy monotonic function is one one.
II : The function f:R+→R defined by f(x)=5+x2 is one one .Solution in Telugu
only I
only II
both I & II
neither I nor II
The correct Answer is:C
Step by step video & text solution for I : Every strictlyy monotonic function is one one. II : The function f:R^(+)rarrR defined by f(x)=5+x^(2) is one one . by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONS BOOK - AAKASH SERIESCHAPTER - FUNCTIONS EXERCISE - EXERCISE -II
165 Videos
- ERRORS AND APPROXIMATIONSBOOK - AAKASH SERIESCHAPTER - ERRORS AND APPROXIMATIONSEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTION
15 Videos
- HEIGHTS AND DISTANCESBOOK - AAKASH SERIESCHAPTER - HEIGHTS AND DISTANCESEXERCISE - PRACTICE SHEET Exercise-I (Level-II) (Straight Objective Type Questions)
13 Videos
Similar Questions
If f(x)=logx,g(x)=x3 then f[g(a)]+f[g(b)]=
View SolutionFind the approximate value of log (2.01) give that log 2 = 0.6934
View SolutionThe angle of elevation of the top of a tower standing on a harzontal plane from the two points lying on a line passing through the foot of the tower at distances a and b respectively are complementary angles. If the line joining the two points sutends an angle θ at the top of the tower, then sinθ is
View SolutionShow that the function f:R→R, defined as f(x)=x2, is neither one-one nor onto.
View SolutionSTATEMENT-1: f(x)=x3 is a one-one function .
and
STATEMENT-2 : Any monotonic function is a one-one function .
View SolutionDetermine whether the functionf:R→(0,∞) defined by f(x)=2x
is one one (or) onto (or) bijection.
View SolutionDetermine whether the function f:R→[0,∞) defined by f(x)=x2 is one one (or)onto (or)bijection.
View SolutionDetermine whether the function f:R→R defined by f(x)=x2 is one one (or) onto (or) bijection.
View SolutionThe function f:R→R is defined as f(x)=3−x. From the following statements,
I. f is one-one
II. f is onto
III. f is a decreasing function the true statements are
View SolutionI : Every strictlyy monotonic function is one one.
II : The function f:R+→R defined by f(x)=5+x2 is one one .
View SolutionThe function f:R→R is defined by f(x)=3−x. Observe the following statements
I. f is one - one
II. f is onto
III. F is a decreasing function
Out of these, true statements are :
View SolutionState which of the following functions are one-one and why? f:R^(+)toR^(+) defined by f(x) =1+x^(2)
View SolutionExamine the function f:R→R be defined by f(x)=3−4x is one one,onto and one one onto.
View SolutionMark (a) if function is one - one and into
Mark (b) if function is one - one and not into
Mark (c) if function is not one - one and into
Mark (d) if function is not one - one and not into
f(x)=x2
f:R+→R+
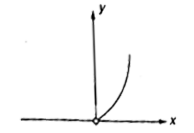
View SolutionMark (a) if function is one - one and into
Mark (b) if function is one - one and not into
Mark (c) if function is not one - one and into
Mark (d) if function is not one - one and not into
f(x)=x2
f:R+→R+

View SolutionStatement 1: f(x)=x3 is a one-one function.
Statement 2: Any monotonic function is a one-one function.
View Solution
