Find the equation of the line passing through the point P(4, 6, 2) and the point of intersection of the line x−13=y2=z+17 and the plane x + y - z = 8.Solution in Punjabi
Step by step video & image solution for Find the equation of the line passing through the point P(4, 6, 2) and the point of intersection of the line frac{x-1}{3}=frac{y}{2}=frac{z+1}{7} and the plane x + y - z = 8. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If [3y−x−2x37] = [5−237],then find x and y
View SolutionFunction 'f:RrarrR,f(x)=3x-5' is :
View SolutionFind the equation of the line passing through the point P(4,6,2) and the point of intersection of the line x−13=y2=z+17 and the plane x+y−z=8.
View SolutionFind the equation of the line passing through the point P(4,6,2) and the point of intersection of the line x−13=y2=z+17and the plane x + y - z = 8 .
View Solutionx−12=y+13=z−14 மற்றும் x−31=y−m2=z என்ற கோடுகள் ஒரு புள்ளியில் வெட்டிக் கொள்ளும் எனில், m-ன் மதிப்பைக் காண்க.
View Solution(2, 3, 6) என்ற புள்ளி வழிச் செல்வதும் x−12=y+13=z−31 மற்றும் x+32=y−3−5=z+1−3 என்ற கோடுகளுக்கு இணையானதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
View Solutionநேர்க்கோடுகள் x−32=y+54=z−1−13 மற்றும் x+13=y−45=z+22என்பது
View Solutionநேர்க்கோடுகள் x+22=y−3=z−14 மற்றும் x−3a=y−14=z−7a செங்குத்து எனில், (→a) -ன் மதிப்பு
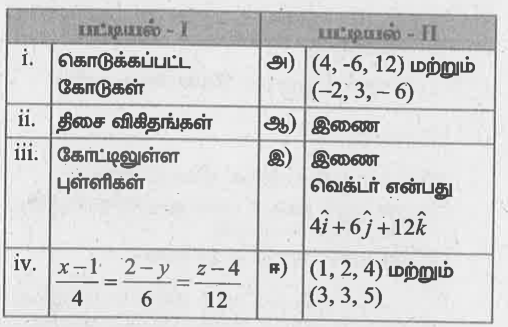
View Solutionபொருத்துக: கோடுகளுக்கு x−14=2−y6=z−412,x−3−2=y−33=5−z6
View SolutionFind the equation of the line passing through the point P(4,6,2) and the point of intersection of the line x−13=y2=z+17 and the plane x+y−z=8.
View SolutionSolve the system of equations. 6x+9y−20z=2 , 4x−6y+5z=1 and 2x+3y+10z=4
View SolutionFind d.r. of the line 4−x2=y6=1−z3
View SolutionFind the equation of the plane passing through the points (-1, 2, 0) , (2, 2, -1) and parallel to the line x−11=2y+12=z+1−1.
View SolutionFind the equation of the plane passing through the points (3,4,1) and (0,1,0) and parallel to the line x+32=y−37=z−25.
View SolutionProve that the lines x+32=y+53=z−7−3 and x+14=y+15=z+1−1 are coplanar. Find the equation of plane containing them.
View Solution
