The accompanying Venn diagram shows three events, A,B, and C, also the probabilities of the various intersections (for instance, P(A∩B)=.07 ). Determine
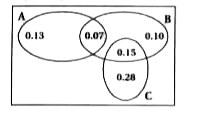
(i) P(A)
(ii) P(B∩C')
(iii) P(A∪B)
(iv) P(A∩B')
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs. Solution in Gujrati
The correct Answer is:(i) 0.20 (ii) 0.17 (iii) 0.45 (iv) 0.13 (v) 0.15 (vi) 0.51
Step by step video, text & image solution for The accompanying Venn diagram shows three events, A,B, and C, also the probabilities of the various intersections (for instance, P(AcapB)=.07 ). Determine (i) P(A) (ii) P(BcapC') (iii) P(AcupB) (iv) P(AcapB') (v) P(BcapC) (vi) Probability of exactly one of the three occurs. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
8 Videos
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Objective type Questions)
12 Videos
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Textbook Illustrations for Practice Work
19 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - NCERT EXEMPLAR PROBLEMS (QUESTION OF MODULE )
11 Videos
- RELATIONS AND FUNCTIONSBOOK - KUMAR PRAKASHANCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Solutions of NCERT Exemplar Problems (Question of Module)
16 Videos
Similar Questions
One urn contains two black balls (labelled B1 and B2 ) and one white ball. A second urn contains one black ball and two white balls (labelled W1, and W2 ). Suppose the following experiment is performed. One of the two urns is chosen at random. Next a ball is randomly chosen from the urn. Then a second ball is chosen at random from the same urn without replacing the first ball.
(i) Write the sample space showing all possible outcomes
(ii) What is the probability that two black balls are chosen ?
(iii) What is the probability that two balls of opposite colour are chosen ?
View SolutionIn a non-leap year's, the probability of having 53 Tuesdays or 53 Wednesdays is
View SolutionTwo coins (a one rupee coin and a two rupee coin) are tossed once. Find a sample space.
View SolutionBy using the principle of mathematical induction , prove the follwing :
P(n)+1+3+5+……….+(2n−1)=n2,n∈N
View SolutionA={−1,0},B={−1,0,1}, then find A×BandB×A
View SolutionIf A and B are mutually exclusive events, P(A)=0.35 and P(B)=0.45, then find
(i) P(A')
(ii) P(B')
(iii) P(A∪B)
(iv) P(A∩B)
(v) P(A∩B')
(vi) P(A'∪B')
View SolutionThe accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections [for instance,P(A∪B)=0.7]. Determine
(i) P (A)
(ii) P(B∩−C)
(iii) P(A∪B)
(iv) P(A∩−B)
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs.
View SolutionThe following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.
View SolutionWhich one of the following pairs would have a larger size ? Explain (i) K " or " K^(+) (ii) Br " or " Br^(-) (iii) O^(2-) " or " F^(-) (iv) Li^(+) " or " Na^(+) (v) P " or "As (vi) Na^(+) " or " Mg^(2+)
View SolutionIf A and B are two events, show that
i) P(A∩BC)=P(A)−P(A∩B)and
ii) the probability that one of them occurs is given by
P(A)+P(B)−2P(A∩B)
View Solutionఏ అవయవాలు కవాటాలు కల్గి ఉంటాయి ?br i) గుండెbr ii) ధమనిbr iii) సిరలుbr iV) శోషరస నాళాలు
View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View SolutionIf A and B are mutually exclusive events, P(A)=0.35 amd P(B)=0.45, then find
(i) P(A')
(ii) P(B')
(iii) P(A∪B)
(iv) P(A∩B)
(v) P(A∩B')
(vi) P(A'∪B')
View SolutionThe accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections [for instance,P(A∪B)=0.7]. Determine
(i) P (A)
(ii) P(B∩−C)
(iii) P(A∪B)
(iv) P(A∩−B)
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs.
View SolutionThe following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.

View Solution
