The moment of inertia of a disc pivoted at its centre about the axis AB as shown in the figure is I. If temperature of disc is increased by ΔT, then moment of inertial of disc about AB increases by
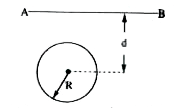
2αIΔT
>2αIΔT
<2αΔT
Can't say anything
The correct Answer is:C
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Geometry Applications5videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Mechanics applications4videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-I (Straight Objective Type Questions) Geometry Applications10videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 333videos
THERMODYNAMICS
Similar Questions
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a then circular disc about an axis passing through its centre and perpendicular to its plane is I. Then, the moment of inertia of the disc about an axis parallel to its diameter and touching the edge of the rim is
View Solution
Knowledge Check
- Question 1 - Select One
A brass disc is rotating about its axis. If temperature of disc is increased then its
Aradius of gyration increases, but moment of inertia remains the sameBmoment of inertia increases but radius of gyration remains the sameCradius of gyration, moment of inertia both remain the sameDradius of gyration, moment of inertia both increase - Question 2 - Select One
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα - Question 3 - Select One
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
Calculate the ratio of moment of inertia of a thin uniform disc about axis 1 and 2 marked in the figure. O is the centre of the disc.
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of an thin circular disc about an axis passing through its center and perpendicualr to its plane, is l. Then, the moment of intertia of the disc about an axis parallel to its diameter and touching the edge of the rim is
View Solution