The angular frequency of the damped oscillator is given by, ω=√(km−b24m2) where k is the spring constant, m is the mass of the oscillatory and b is the damping constant. If the ratio b2mk is 8%, the change in time period compared to the undamped oscillator is approximately as follows:
increases by 1%
increases by 8%
decreases by 1%
decreases by 8%
The correct Answer is:A
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:PRACTICE EXERCISE - EQUATIONS OF SHM
Explore 33 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:PRACTICE EXERCISE - SIMPLE PENDULUM
Explore 22 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE -II SPRINGS
Explore 19 Videos
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 12 Videos
- PHYSICAL WORLDBook:AAKASH SERIESChapter:PHYSICAL WORLDExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
The angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View Solution
Knowledge Check
The angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
Aincreases by 1%Bincreases by 8%Cdecreased by 1%DdecreaseFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10 g s^(-1) The time period of oscillation is (approx.)
A2πsB2π13sCπ5sDπ√5sA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
A2π3√10MKB4π√M3KC4π√MKD2π√M3K
For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
The period of oscillation
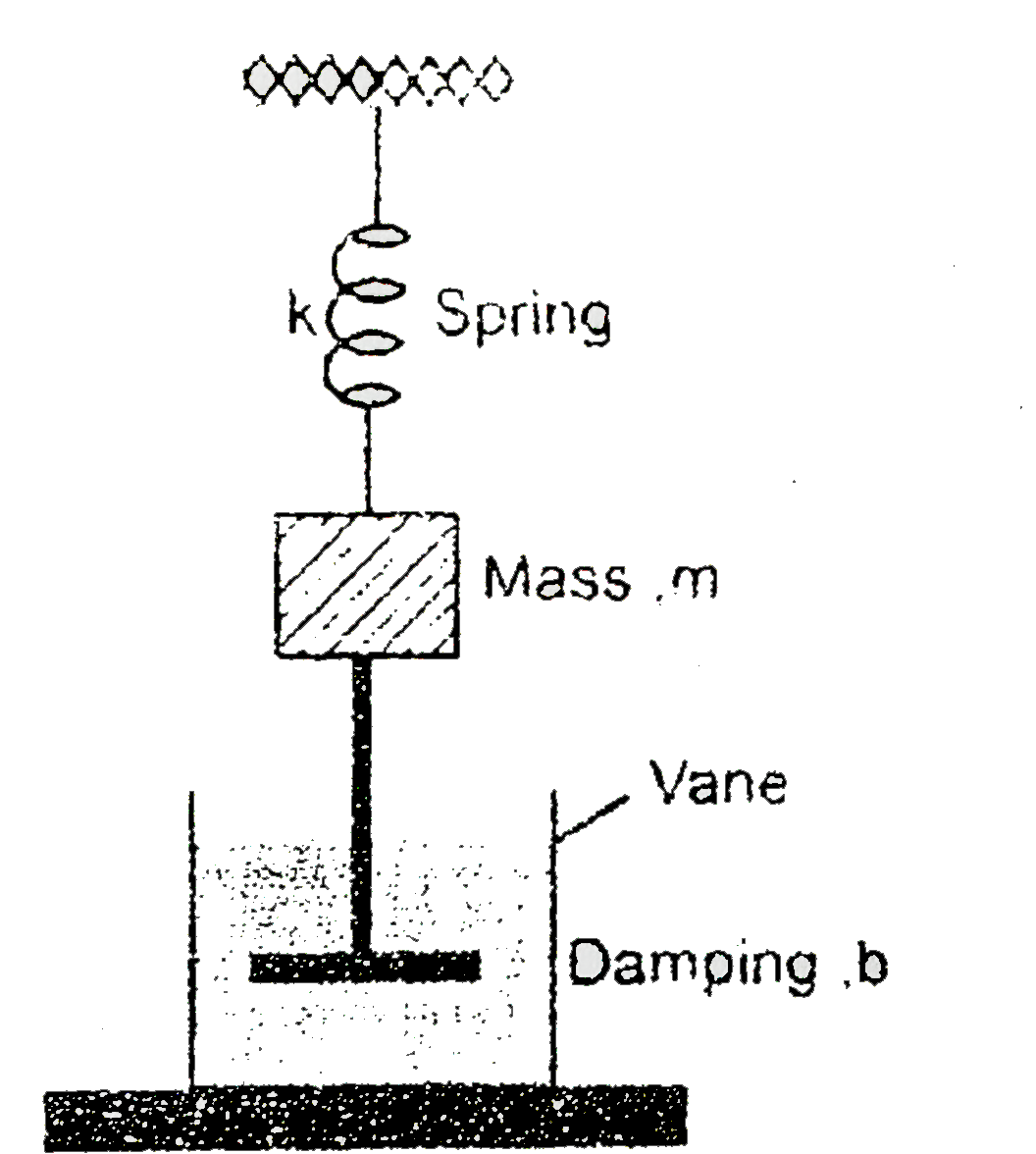
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
What is the period of the motion?
View SolutionFor the damped oscillator shown in previous figure, k=180Nm−1 and the damping constant b is 40gs−1 .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than √km).
View SolutionFor a damped oscillator the mass 'm' of the block is 200 g, k = 90 N m−1 and the damping constant b is 40 g s−1. Calculate the period of oscillation.
View Solution

